Multivariate Calculus
&
Ordinary Differential Equations
Lecture 14
1 Ordinary Differential Equations
1.8.4 Critical damping
For $p=\omega$ the characteristic equation
$ \lambda^2+2p\lambda+\omega^2=0 $
has one root of multiplicity two: $\lambda=-p$. Two linearly independent solutions are thus
$ e^{-p t}\quad\text{and}\quad te^{-p t} $
and the general solution is
$x(t)=e^{-p t}(c_1+c_2 t). $
1 Ordinary Differential Equations
1.8.4 Critical damping
$x(t)=e^{-p t}(c_1+c_2 t). $
Unlike the underdamped spring it is straightforward to express $c_1$ and $c_2$ in terms of the initial conditions $x(0)$ and $x'(0)$:
$ c_1=x(0) \quad\text{and}\quad c_2=x(0)p+x'(0). $
Therefore $\,x(t)=e^{-p t}( x(0)+x(0)pt+x'(0)t ).$
The linear polynomial $x(0)+x(0)pt+x'(0)t$ vanishes for
$\ds t=-\frac{x(0)}{x(0)p+x'(0)}.$
This corresponds to a positive time $t$ if $x'(0)\lt -x(0) p.$
1 Ordinary Differential Equations
1.8.4 Critical damping
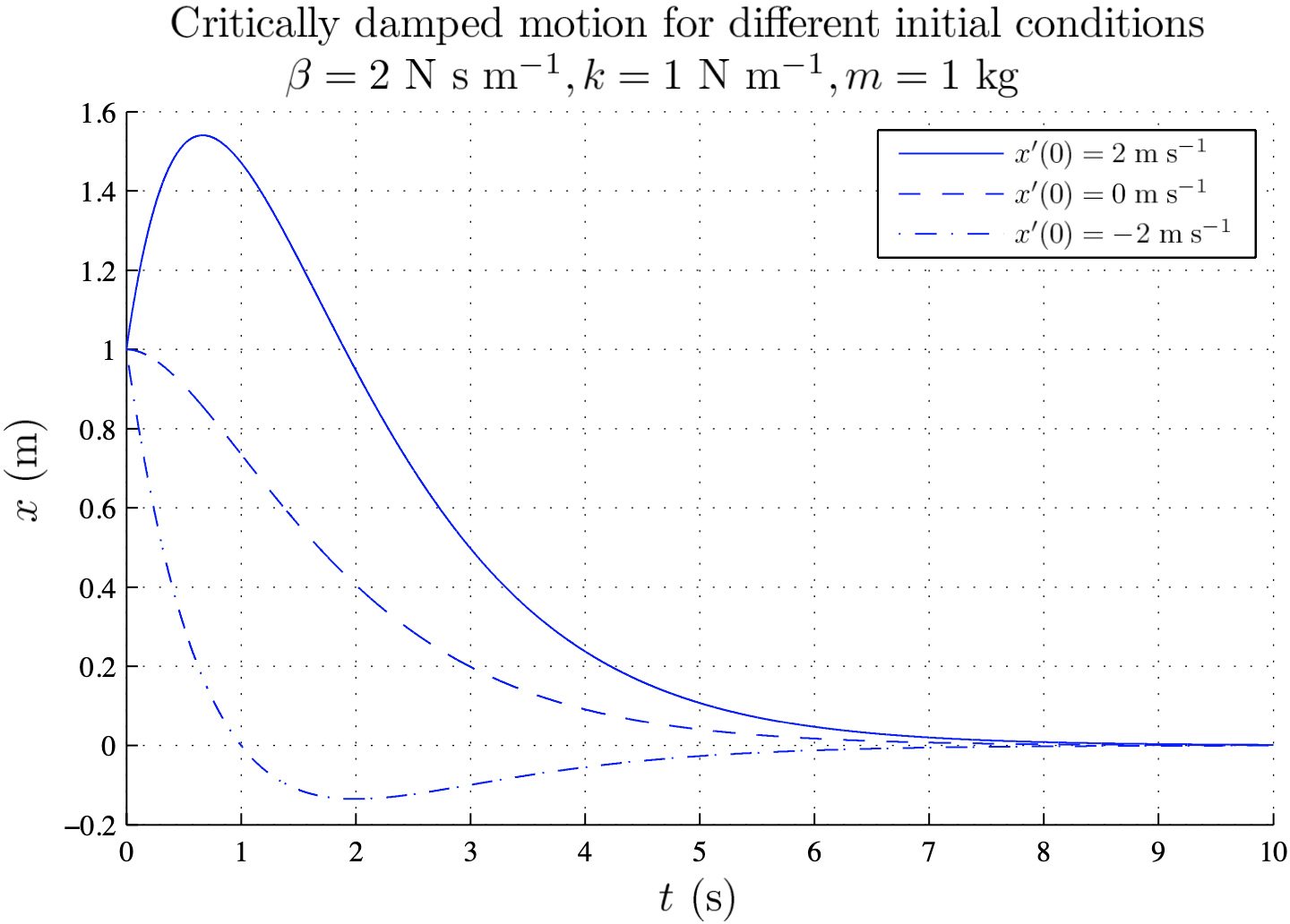
Depending on the initial conditions, the critically-damped spring behaves as shown in this figure:
1 Ordinary Differential Equations
1.8.4 Critical damping

• The top-most curve corresponds to $x(0)$ and $x'(0)$ both positive, so that the weight is not just pulled down a distance $x(0)$ but is also given a downward kick on release.
• The middle curve corresponds to $x'(0)=0$ so that we only pull down the weight and then release it.
• The third curve corresponds to $x'(0)\lt 0$ so that upon release the weight is kicked upward. Since the spring overshoots the equilibrium we must also have that $x'(0)\lt -x(0) p$.
1 Ordinary Differential Equations
1.8.4 Critical damping
1 Ordinary Differential Equations
1.8.4 Critical damping
Example: A mass of $1$kg is attached to a spring hanging under gravity, with spring constant $4$. What value of the damping constant implies critical damping?
Again we use $\,\ds x''+ \frac{\beta}{m}x' +\frac{k}{m}x = 0.$
Since $m=1\,$ and $\,k=4,\,$ then $\ds \,\ds x''+\beta x' +4x = 0.$
1 Ordinary Differential Equations
1.8.4 Critical damping
Example: A mass of $1$kg is attached to a spring hanging under gravity, with spring constant $4$. What value of the damping constant implies critical damping?
Since $m=1\,$ and $\,k=4,\,$ then $\ds \,\ds x''+\beta x' +4x = 0.$
Characteristic equation: $\, \lambda^2 + \beta \lambda + 4 = 0.$
Solution: $\ds\; \lambda = \frac{-\beta\pm \sqrt{\beta^2 - (4)(4)}}{2}$
We have critical damping when $\ds\, \beta^2 =16\,$ or $\,\beta = 4.$
1 Ordinary Differential Equations
1.8.5 Overdamping
For $p\gt \omega$ the characteristic equation
$ \lambda^2+2p\lambda+\omega^2=0 $
has two distinct real roots
$ \lambda_1 =-p-\sqrt{p^2-\omega^2}=:-\alpha $
$ \lambda_2 =-p+\sqrt{p^2-\omega^2}=:-\beta $
with $\alpha>\beta>0$.
1 Ordinary Differential Equations
1.8.5 Overdamping
$ \lambda_1 =-p-\sqrt{p^2-\omega^2}=:-\alpha $
$ \lambda_2 =-p+\sqrt{p^2-\omega^2}=:-\beta $
Two linearly independent solutions are thus
$ e^{-\alpha t}\quad\text{and}\quad e^{-\beta t} $
and the general solution is
$\ds x(t)=c_1e^{-\alpha t}+c_2e^{-\beta t}.$
For generic initial conditions $x(0)$ and $x'(0),$ the constants $c_1$ and $c_2$ are both nonzero.
1 Ordinary Differential Equations
1.8.5 Overdamping
Assuming this, we have that for sufficiently large $t$
$x(t)_{\text{critial damping}}\sim c_2 t e^{-p t}$
and
$x(t)_{\text{overdamped}}\sim c_2 e^{-\beta t}.$
Since $\beta=p-\sqrt{\dots}\lt p$ we see that the overdamped spring takes longer to return to equilibrium than the critically damped spring.
1 Ordinary Differential Equations
1.8.5 Overdamping
The overdamped spring describes a door-closer that is too tight. It may take a long time for the door to actually close because the strong damping restricts (nearly) all movement.
A tradeswoman will try to adjust a door-closer such that the damping will be as close as possible to critical damping. As always, Maths Rules!
1 Ordinary Differential Equations
1.8.5 Overdamping
Example: A mass of $1$kg is attached to a spring hanging under gravity with damping constant $5$ and spring constant $4$. Find the position of the mass after time $t$ if it is pulled down $1$m from the equilibrium position and released without kick.
Once again $\,\ds x''+ \frac{\beta}{m}x' +\frac{k}{m}x = 0$
Here $\,m = 1,$ $\,\beta = 5,$ $\,k = 4.$
Initial conditions: $x(0)=1,$ $\,x'(0)=0.$
1 Ordinary Differential Equations
1.8.5 Overdamping
$\ds x''+ \frac{\beta}{m}x' +\frac{k}{m}x = 0;$ $\;m = 1,$ $\,\beta = 5,$ $\,k = 4.$
Initial conditions: $x(0)=1,$ $\,x'(0)=0.$
Thus $\;\ds x''+ 5x' + 4x = 0. $ What is the solution $x(t)$?
Characteristic equation: $\;\ds \lambda^2+ 5\lambda +4 = 0. $
$\ds \Ra \left(\lambda+ 4\right)\left(\lambda+ 1\right)=0$ $\ds \;\Ra \lambda = -1,-4.$
1 Ordinary Differential Equations
1.8.5 Overdamping
Initial conditions: $x(0)=1,$ $\,x'(0)=0.$
$\ds \;\Ra \lambda = -1,-4.$
General sol: $\ds x(t) = \ds c_1 e^{-t}+ c_2 e^{-4t}. $
$\ds x(0) = 1 $ $\ds = c_1 + c_2 \;$ (Equation 1)
$\ds x'(t) = $ $\ds-c_1 e^{-t} - 4 c_2 e^{-4t}$
$\ds x'(0) = 0 $ $\ds = - c_1 -4 c_2\;$ (Equation 2)
Solving the system: $\ds c_1 = \frac{4}{3}\,$ and $\,c_2=\ds-\frac{1}{3}.$
1 Ordinary Differential Equations
1.8.5 Overdamping
Example: A mass of $1$kg is attached to a spring hanging under gravity with damping constant $5$ and spring constant $4$. Find the position of the mass after time $t$ if it is pulled down $1$m from the equilibrium position and released without kick.
Using $\ds c_1 = \frac{4}{3}\,$ and $\,c_2=\ds-\frac{1}{3},$
we obtain the solution $\ds\; x(t) = \frac{4}{3}e^{-t} -\frac{1}{3}e^{-4t}.$
1 Ordinary Differential Equations
1.8.5 Overdamping
1 Ordinary Differential Equations
1.8.6 Summary of motion of a spring:
The equation of motion of a mass $m$ attached to a damped spring is described by the ODE
$\ds x''+2p\,x'+\omega^2 x=0,$
where
$\ds \omega^2=\frac{k}{m}>0, \quad 2p=\frac{\beta}{m}>0$
and $k$ is the spring constant and $\beta$ the damping constant.
1 Ordinary Differential Equations
1.8.6 Summary of motion of a spring:
The roots of the characteristic equation $\lambda^2+2p\lambda+\omega^2=0$ determine the type of motion:
-
$p=0$; No damping - pure oscillatory or harmonic motion.
The roots are $\pm i \omega$ and the general solution is given by \[ x(t)=c_1\cos(\omega t)+c_2\sin(\omega t)=A\cos(\omega t-\phi). \] -
$p\lt \omega$; Underdamped motion.
The roots are $-p\pm i \omega_p$, $\omega_p=\omega\sqrt{1-(p/\omega)^2}$ and the general solution is given by \[ x(t)=e^{-pt} \Bigl(c_1\cos(\omega_p t)+c_2\sin(\omega_p t)\Bigr) =A e^{-pt}\cos(\omega_pt-\phi). \]
1 Ordinary Differential Equations
1.8.6 Summary of motion of a spring:
The roots of the characteristic equation $\lambda^2+2p\lambda+\omega^2=0$ determine the type of motion:
-
$p=\omega$; Critically damped motion.
The single root (of multiplicity $2$) is given by $-p$ and the general solution is given by \[ x(t)=e^{-pt}(c_1+c_2t). \] -
$p>\omega$; Overdamped motion.
The two roots (denoted $-\alpha$ and $-\beta$) are $-p\pm \sqrt{p^2-\omega^2}$ and the general solution is given by \[ x(t)= c_1e^{-\alpha t}+c_2e^{-\beta t}. \]
Summary: $\,x''+\frac{\beta}{m}x'+\frac{k}{m}x=0\,\Ra$ $\,\lambda^2+\frac{\beta}{m}\lambda+\frac{k}{m}=0$
$\beta=0$ - No damping. Two purely imaginary roots: $\pm i \omega.$
$ \ds \quad \textbf{Sol:} \; x(t)=c_1\cos(\omega t)+c_2\sin(\omega t)=A\cos(\omega t-\phi). $
$\beta^2\lt 4 km$ - Underdamped. Two complex roots: $-p\pm i \omega_p,$
$ \ds \quad \textbf{Sol:}\; x(t)=e^{-pt} \Bigl(c_1\cos(\omega_p t)+c_2\sin(\omega_p t)\Bigr) =A e^{-pt}\cos(\omega_pt-\phi). $
$\beta^2= 4 km$ - Critically damped. Single real root: $-p.$
$ \ds \quad \textbf{Sol:}\; x(t)=e^{-pt}(c_1+c_2t). $
$\beta^2\gt 4 km$ - Overdamped. Two real roots ($-\alpha$, $-\beta$): $-p\pm \sqrt{p^2-\omega^2}.$
$ \ds \quad \textbf{Sol:}\; x(t)= c_1e^{-\alpha t}+c_2e^{-\beta t}. $