If you try the "spring-weight" system at home it is unlikely to display true simple harmonic motion. If that were possible you could build a perpetuum mobile.

To make the model more realistic we need to take into account the effect of damping. This is caused by air-resistance and mechanical friction of the spring.

The most common model of damping assumes that it corresponds to a force $F_d,$ proportional to the velocity of the moving object, and opposite to the direction of movement. Hence

where $\beta>0$ is the damping constant measured in $\text{N s m}^{-1}.$

The total force $F$ for the damped spring is thus given by

As before, $k s=m g,$ so that

Thanks to Newton's second law this yields the equation of motion

Thanks to Newton's second law this yields the equation of motion

This equation only depends on the ratios of $k/m$ and $\beta/m,$ and it is customary to not only set

Then the equation of motion for the damped spring is given by

This is a homogeneous second-order linear ODE with constant coefficients.

The corresponding characteristic equation is given by

which has discriminant

There are three different cases to consider.

• $D\lt 0$ (i.e., $p\lt \omega$).
  This is the underdamped or weakly-damped spring.
• $D=0$ (i.e., $p=\omega$).
  This is the critically-damped spring.
• $D>0$ (i.e., $p>\omega$).
  This is the overdamped or strongly-damped spring.

For $p\lt \omega$ the characteristic equation

has two complex conjugate roots

Two linearly independent solutions are thus

where

The general solution is

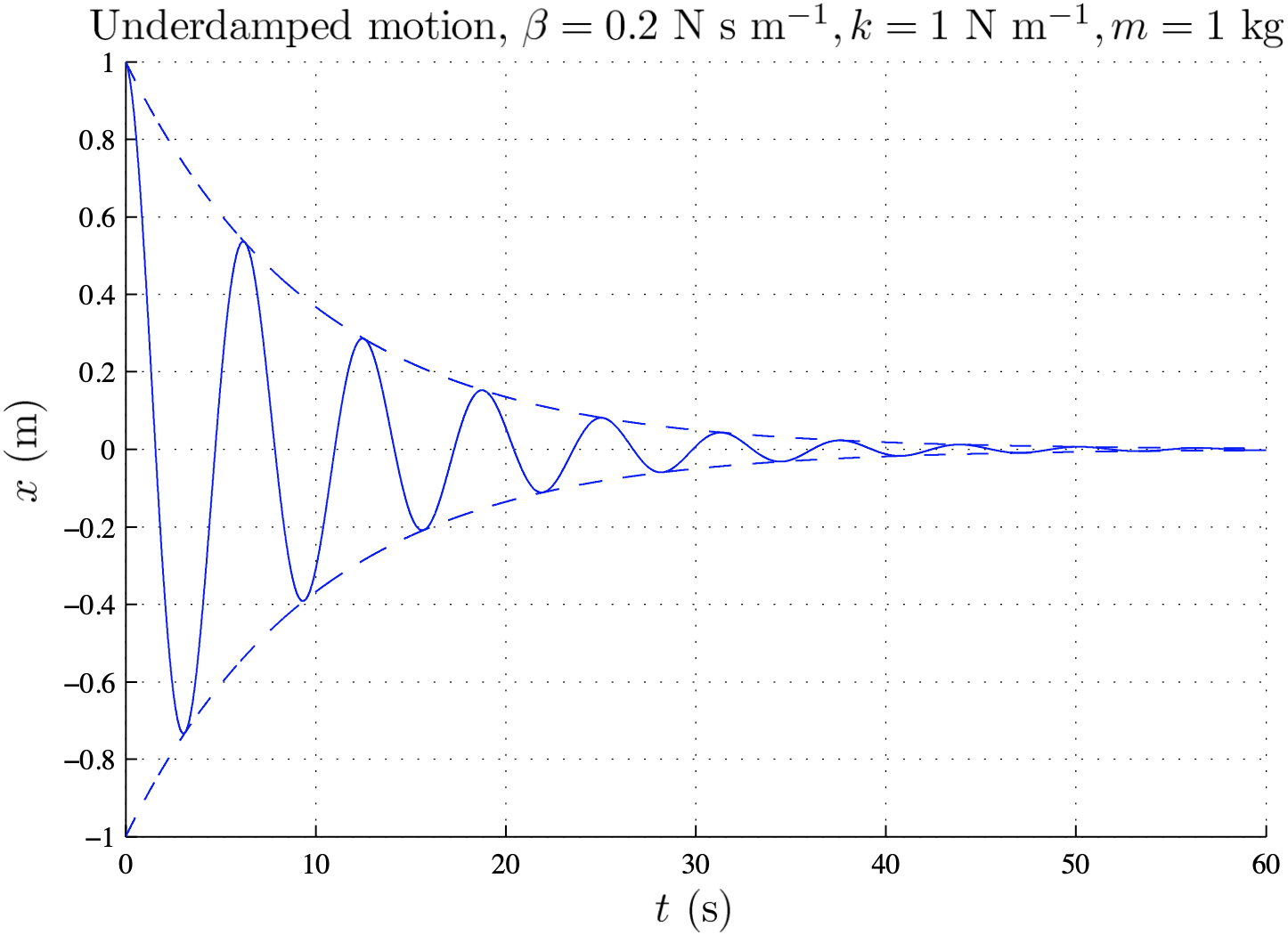
This figure shows an example of underdamped motion:

It is best to write the general solution in terms of a single trigonometric function:

Here $A(t)$ is a time-dependent amplitude (as shown in the above figure with the dashed lines):

and $\omega_p$ is the frequency of the underdamped spring.

Since

the damping of the spring leads to a frequency red-shift and an increase in the period of the spring.

When $p$ approaches $\omega$ the period tends to infinity so that we may expect that the critically-damped spring does not display oscillatory motion. This is the case considered in the next section.

Example: A mass of $1$kg is attached to a spring hanging under gravity with damping constant $0.2$ and spring constant $4$. Find the position of the mass after time $t$ if it is pulled down $1$m from the equilibrium position and released without kick.

Recall $\,\ds x''+ \frac{\beta}{m}x' +\frac{k}{m}x = 0$

Then $\,m = 1,$ $\,\beta = 0.2,$ $\,k = 4.$

Initial conditions: $x(0)=1,$ $\,x'(0)=0.$

Example: A mass of $1$kg is attached to a spring hanging under gravity with damping constant $0.2$ and spring constant $4$. Find the position of the mass after time $t$ if it is pulled down $1$m from the equilibrium position and released without kick.