MATH3401
Complex Analysis
Lecture 20
Contour integrals
Further examples
Example 4: Evaluate \(I = \ds \int_C \frac{dz}{z}\), where \(C= 2e^{i\theta}\), \(0\leq \theta \leq 2 \pi\).
Can't repeat argument from Example 3 directly.
|
\(I = I_1 + I_2\) where \(I_j = \ds \int_{C_j}\frac{dz}{z}\) |
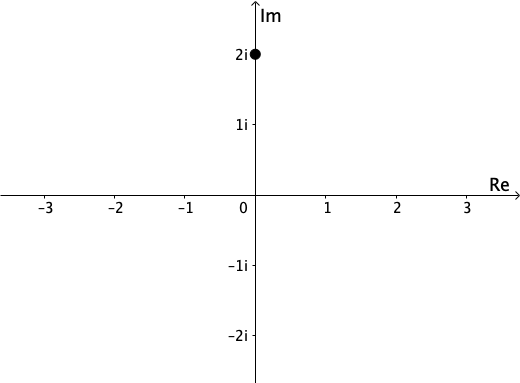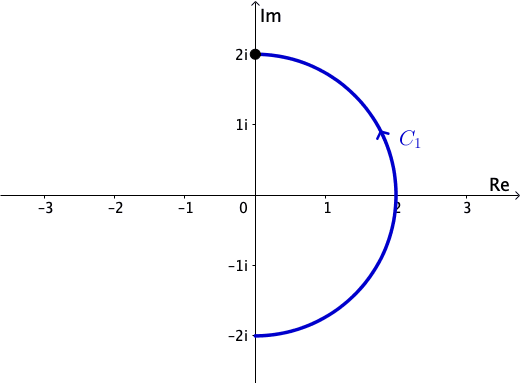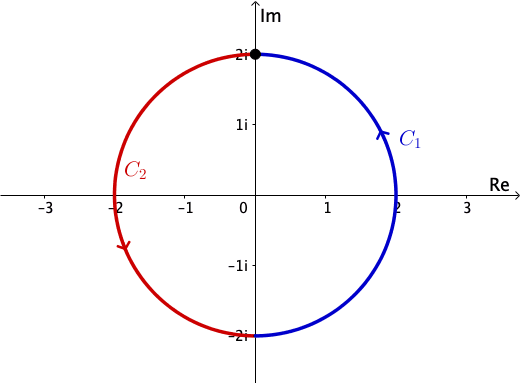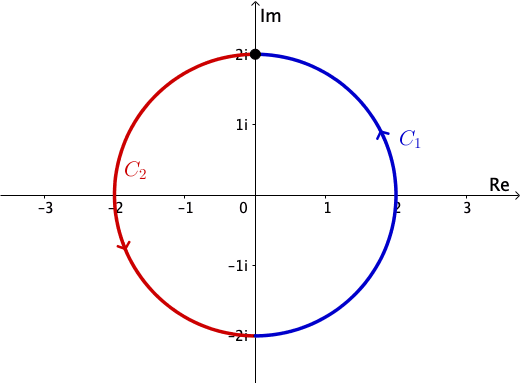
|
Contour integrals
Further examples
Example 4 (cont): On \[D = \C \setminus \{\text{negative real axis}\cup \{0\}\},\] \(\Log z\) is a primitive for \(\dfrac{1}{z}\). \(C_1\subset D\), so Theorem in Lecture 19 \(\Rightarrow\)
\(I_1 = \Log(2i)-\Log(-2i)\) \(= \ln|2i| + i\dfrac{\pi}{2}-\left(\ln|-2i| + i\left(-\dfrac{\pi}{2}\right)\right)\)
\(\quad = \pi i\).
Remark: Agrees with calculation from Lecture 19, Example 1.
Contour integrals
Further examples
Example 4 (cont): For \(I_2\), on \[D' = \C \setminus \{\text{positive real axis}\cup \{0\}\},\] \(1/z\) has a primitive, e. g. \(\mathcal \Log z = \ln|z| + i \,{\Large\mathcal a}\mathcal rg(z) \), \(0 \leq {\Large\mathcal a}\mathcal rg(z) < 2 \pi\).
Note \(C_2 \subset D'\). So Theorem in Lecture 19 \(\Rightarrow\)
\(I_2 = \mathcal \Log(-2i)-\mathcal \Log(2i)\) \( = \ln 2 + i\dfrac{3\pi}{2}-\left(\ln 2 + i\left(\dfrac{\pi}{2}\right)\right)\)
\(\quad = \pi i\).
Thus \(I= I_1 + I_2 = 2 \pi i\).
Contour integrals
Further examples
Example 4 (cont): So \[ \int_C z^n dz = \left\{ \begin{array}{lr} 0 & n\in \Z\setminus \{-1\}\\ 2 \pi i & n=-1 \end{array} \right. \]
for any circle \(C\) centred at the origin, positively oriented.
Cauchy-Goursat
Let \(C\) be a simple closed curve in \(\C\). If \(f\) is analytic on \(C\) and its interior, then \[ \int_C f\left(z\right)dz = 0. \]
Cauchy-Goursat
Remark: \(\ds \int_C f\left(z\right)dz = 0\) \(\nRightarrow\) \(f\) is analytic in and on \(C\).
e. g. \(\ds \int_C z^n dz = 0\), \(n= -2, -3, -4, \ldots \)
Proof of C-G: Do it for
Cauchy-Goursat
Key step in proof: \(M\)-\(\ell\) estimate
Suppose \(f\) is continuous on a contour \(C\) given by \(z = z(t)\), \(a\leq t \leq b\). Then exists \( M\) such that \[ |f\left(z\right)| \leq M \quad \forall z\in\C, \]
via extreme value theorem in \(\R\).
Cauchy-Goursat
So \(\ds \int_C f \left(z\right) dz =\left| \ds \int_a^b f \left(z \left(t\right)\right) z' \left(t\right) dt\right|\)
\(\qquad \qquad \quad \leq \ds \int_a^b \left| f \left(z \left(t\right)\right) \right| \cdot \left| z' \left(t\right)\right|dt \)
\(\qquad \qquad \quad \leq M \ds \int_a^b \left| z' \left(t\right)\right|dt \) \(= M \ell\).
where \(\ell = \ell\left(C\right)=\text{length}\) of \(C\).
Cauchy-Goursat
Recall: a domain \(D\) is simply connected if for every simple closed contour \(C\) in \(D\), there holds \[ \text{Int}\, C \subset D. \]
i. e. "no holes". In other words, all simple closed contours are null homotopic.
If \(D\) is not simply connected, it is multiply connected.
Cauchy-Goursat extension
Multiply connected domains
If \(f\) is analytic on simple closed contours \(C\), \(C_1, C_2, \ldots, C_n\subset \text{Int}\, C\), and the interior of the domain bounded by \(C_1, C_2, \ldots, C_n\), with \(C\) positively oriented and \(C_k\) negatively oriented, then \[ \int_C f + \sum_{j=1}^{n} \int_{C_j} f = 0. \]