Mathematical Analysis

Lecture 2

1.3 Archimedean property & Density of $\Q$

Theorem 1.3.1.

  1. (Archimedean property) If $x, y \in \R$ and $x \gt 0$, then there exists an $n \in \N$ such that \begin{equation*} nx \gt y . \end{equation*}
  2. ($\Q$ is dense in $\R$) If $x, y \in \R$ and $x \lt y,$ then there exists an $r \in \Q$ such that $x \lt r \lt y.$



Proof of the Archimedean property

  1. (Archimedean property) If $x, y \in \R$ and $x \gt 0$, then there exists an $n \in \N$ such that \begin{equation*} nx \gt y . \end{equation*}

We will prove it by contradiction. That is, suppose that $x,y\in\R$ with $x>0$ and for every $n\in\N$ we have that

$ nx\leq y. $

Then $y$ would be an upper bound of $A:= \{nx:n\in \N\}.$


Proof of the Archimedean property

Then $y$ would be an upper bound of $A:= \{nx:n\in \N\}.$

But then $A$ has a least upper bound in $\R.$

Set $\alpha:= \sup\, A.$ Since $x>0$, then $\alpha - x \lt \alpha$, and $\alpha - x$ is not an upper bound of $A$. Hence

$\alpha -x \lt mx\,$ for some $\,m\in \N$.

But then $\alpha \lt (m+1)x$ $\in A,$ which is impossible, since $\alpha$ is an upper bound of $A.$ This is a contradiction❗

Therefore, the statement (1) must be true. $\;\bs$



Proof of the Density of $\Q$

  1. ($\Q$ is dense in $\R$) If $x, y \in \R$ and $x \lt y,$ then there exists an $r \in \Q$ such that $x \lt r \lt y.$

Case 1: First assume $0 \leq x \lt y$. A rational number is a quotient of integers, so our goal is to produce $m,n\in \N$ so that \begin{equation} x \lt \frac{m}{n} \lt y \qquad (1.1) \end{equation}


Proof of the Density of $\Q$

Case 1: First assume $0 \leq x \lt y$. A rational number is a quotient of integers, so our goal is to produce $m,n\in \N$ so that \begin{equation} x \lt \frac{m}{n} \lt y \qquad (1.1) \end{equation}

Using (1) we may pick $n\in \N$ large enough so that $$ \dfrac{1}{n} \lt y-x. \qquad (1.2) $$ Multiplying (1.1) by $n$ gives $nx\lt m \lt ny$.


Proof of the Density of $\Q$

Case 1: First assume $0 \leq x \lt y$.
$ \qquad \qquad \qquad nx\lt m \lt ny \quad (1.1) $

With $n$ already chosen, the idea now is to choose $m$ to be the smallest natural number greater than $nx$. In other words, pick $m\in \N$ such that \begin{equation*} m-1 \overset{(*)}{\le} n x \overset{(**)}{\lt} m . \end{equation*} Now, inequality ($**$) immediately implies $x \lt \dfrac{m}{n}$.




Proof of the Density of $\Q$

Case 1: First assume $0 \leq x \lt y$.

                   👉   $x \lt \dfrac{m}{n}$

$nx\lt m \lt ny \quad (1.1)$
$ \dfrac{1}{n} \lt y-x. \quad (1.2) $
$ m-1 \overset{(*)}{\le} n x \overset{(**)}{\lt} m . $

Now inequality (1.2) is equivalent to $x\lt y-\dfrac{1}{n},$ we can use ($*$) to write

$m \leq n x +1$ $\lt n\left( y-\dfrac{1}{n}\right)+1$ $= n y.$

Since $m \lt n y$ implies $\dfrac{m}{n} \lt y$, we have that $x \lt \dfrac{m}{n} \lt y.$



Proof of the Density of $\Q$

Case 1: First assume $0 \leq x \lt y$.

Since $m \lt n y$ implies $\dfrac{m}{n} \lt y,$ we have that $x \lt \dfrac{m}{n} \lt y.$

Setting $r=\dfrac{m}{n}\in \Q,$ we have that $$x \lt r \lt y.$$






Proof of the Density of $\Q$

Case 2: We assume that $x \lt 0$.

If $y > 0$, then just take $r=0$.

If $y \leq 0$, then \[ 0 \leq -y \lt -x, \] and we find a rational $q$ such that $-y \lt q \lt -x$.

We can use $\,r = -q\,$ from Case 1. $\,\blacksquare$




Example 1.3.1

Claim: $\inf\, \left\{\dfrac{1}{n} : n\in \N\right\} = 0$.

Proof. Let $A := \left\{ \dfrac{1}{n} : n \in \N \right\}$. Notice that $A$ is not empty. Moreover, $\dfrac{1}{n} > 0$ for all $n \in \N,$ and so 0 is a lower bound.

This means that $b := \inf\, A$ exists. As 0 is a lower bound, then $b \geq 0.$



Example 1.3.1

Claim: $\inf\, \left\{\dfrac{1}{n} : n\in \N\right\} = 0$.

Proof. Now take an arbitrary $a > 0$.

By the Archimedean property there exists an $n$ such that $na > 1$, or in other words $a > \dfrac{1}{n}$ $\in A$.

Therefore, $a$ cannot be a lower bound for $A$.

Hence $b=0.$ $\;\blacksquare$



Example 1.3.2.

Claim: There exists a unique positive number $r\in \R$ such that $r^2=2$. We denote $r = \sqrt{2}$.




👀 Complementary reading 📖




1.4 Using supremum and infimum

Suprema and infima are compatible with algebraic operations. For a set $A \subset \R$ and $x \in \R$ define \begin{align*} x + A & := \{ x+y \in \R : y \in A \} , \\ xA & := \{ xy \in \R : y \in A \} . \end{align*} For example, if $A = \{ 1,2,3 \}$, then

$5+A = \{ 6,7,8 \}\;$ and $\;3A = \{ 3,6,9\}$.




1.4 Using supremum and infimum

Theorem 1.4.1. Let $A \subset \R$ be nonempty and $x\in \R$.

  1. If $A$ is bounded above, then $\sup (x+A) = x + \sup\, A$.
  2. If $A$ is bounded below, then $\inf (x+A) = x + \inf\, A$.
  3. If $x \gt 0$ and $A$ is bounded above, then $\sup (xA) = x ( \sup\, A )$.
  4. If $x \gt 0$ and $A$ is bounded below, then $\inf (xA) = x ( \inf\, A )$.
  5. If $x \lt 0$ and $A$ is bounded below, then $\sup (xA) = x ( \inf\, A )$.
  6. If $x \lt 0$ and $A$ is bounded above, then $\inf (xA) = x ( \sup\, A )$.


1. If $A$ is bounded above, then $\sup (x+A) = x + \sup\, A$.

Proof. Assume $b$ is an upper bound for $A$. That is, $y \leq b$ for all $y \in A$. Then $x+y \leq x+b$ for all $y \in A$, and so $x+b$ is an upper bound for $x+A$. In particular, if $b = \sup\, A$, then \begin{equation*} \sup (x+A) \leq x+b = x+ \sup\, A . \end{equation*} In the other hand, if $b$ is an upper bound for $x+A$, then $x+y \leq b$ for all $y \in A$ and so $y \leq b-x$ for all $y \in A$. So $b-x$ is an upper bound for $A$. If $b =\sup (x+A),$ then \begin{equation*} \sup\, A \leq b-x = \sup (x+A) -x . \;\bs \end{equation*}


1.5 Absolute value

The absolute value is defined as \begin{equation*} \abs{x} := \begin{cases} x & \text{if } x \geq 0, \\ -x & \text{if } x \lt 0 . \end{cases} \end{equation*}




👀 Complementary reading 📖


1.5 Absolute value

Theorem 1.5.1.

  1. $\abs{x} \geq 0$, moreover, $\abs{x}=0$ if and only if $x = 0$.
  2. $\abs{-x} = \abs{x}$ for all $x \in \R$.
  3. $\abs{xy} = \abs{x}\abs{y}$ for all $x,y \in \R$.
  4. $\abs{x}^2 = x^2$ for all $x \in \R$.
  5. $\abs{x} \leq y$ if and only if $-y \leq x \leq y$.
  6. $-\abs{x} \leq x \leq \abs{x}$ for all $x \in \R$.

Proof. 📝 = Exercise!

👀 Complementary reading 📖



1.5 Absolute value

Theorem 1.5.2. (Triangle Inequality) $$\abs{x+y} \leq \abs{x}+\abs{y}$$ for all $x, y \in \R$.




👀 Complementary reading 📖


1.5 Absolute value

Corollary 1.5.3.

  1. Reverse triangle inequality: $$\qquad \qquad \bigl\lvert (\abs{x}-\abs{y}) \bigr\rvert \leq \abs{x-y}.$$
  2. $\abs{x-y} \leq \abs{x}+\abs{y}$.

Proof. 📝 For part 1, plug $x=a-b$ and $y = b$ into the standard triangle inequality, and use Theorem 1.5.1.
For part 2, replace $y\,$ by $-y\,$ in the standard triangle inequality.

👀 Complementary reading 📖



1.5 Absolute value

Corollary 1.5.4. Let $x_1, x_2, \ldots, x_n \in \R$. Then \begin{equation*} \abs{x_1 + x_2 + \cdots + x_n} \leq \abs{x_1} + \abs{x_2} + \cdots + \abs{x_n} . \end{equation*}

Proof. 📝 Use induction. 😃




👀 Complementary reading 📖


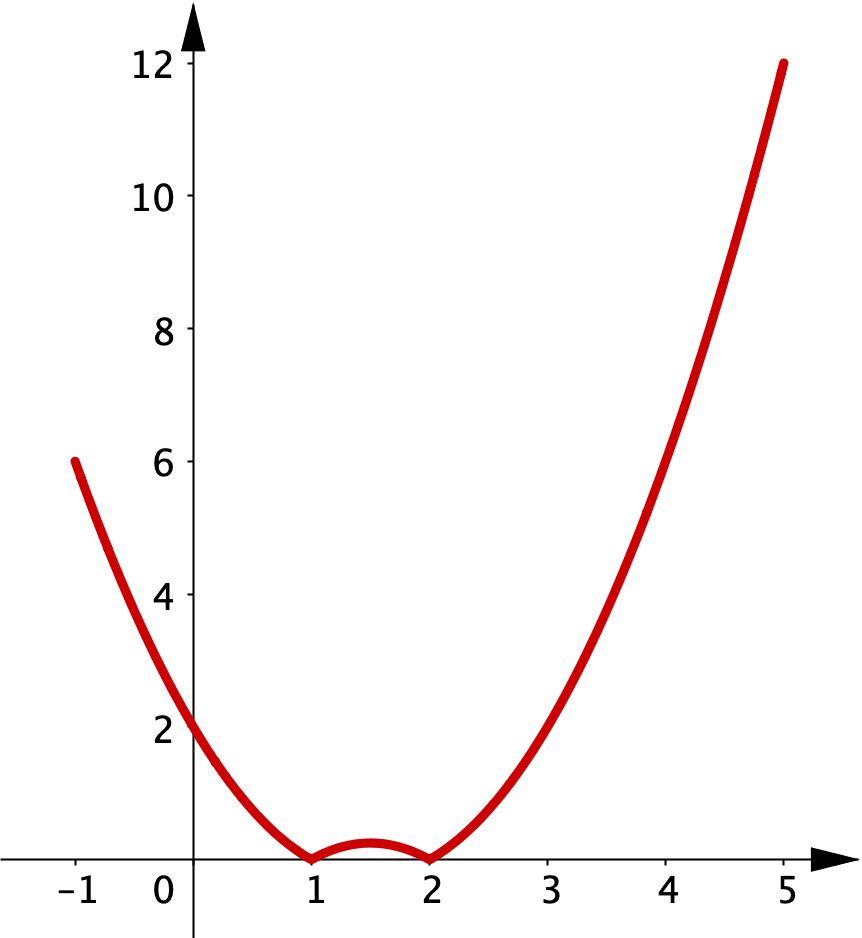
Example 1.5.1.

Find a number $M$ such that $\sabs{x^2-3x+2} \leq M$ for all $-1 \leq x \leq5$.

By the triangle inequality,

$\sabs{x^2-3x+2}$ $ \leq \sabs{x^2}+\sabs{3x}+\sabs{2}$ $ = \sabs{x}^2+3\sabs{x}+2 .$

Note that the expression $\sabs{x}^2+3\sabs{x}+2$ is largest when $\abs{x}$ is largest. In the interval provided, $\abs{x}$ is largest when $x=5$ and so $\abs{x}=5$. One possibility for $M$ is

$M$ $ = 5^2+3(5)+2$ $ = 42 .$

👀 Complementary reading 📖



Example 1.5.1.

Find a number $M$ such that $\sabs{x^2-3x+2} \leq M$ for all $-1 \leq x \leq5$.

$M$ $ = 5^2+3(5)+2$ $ = 42 .$



1.5 Absolute value

Definition 1.5.1. Suppose $f \colon D \to \R$ is a function. We say $f$ is bounded if there exists a number $M$ such that $\abs{f(x)} \leq M$ for all $x \in D$.


Credits