To be continuous or not to be? 🧐
|
|
|
| Example A | Example B | Example C |
To be continuous or not to be? 🧐

To be continuous or not to be? 🧐

To be continuous or not to be? 🧐

To be continuous or not to be? 🧐
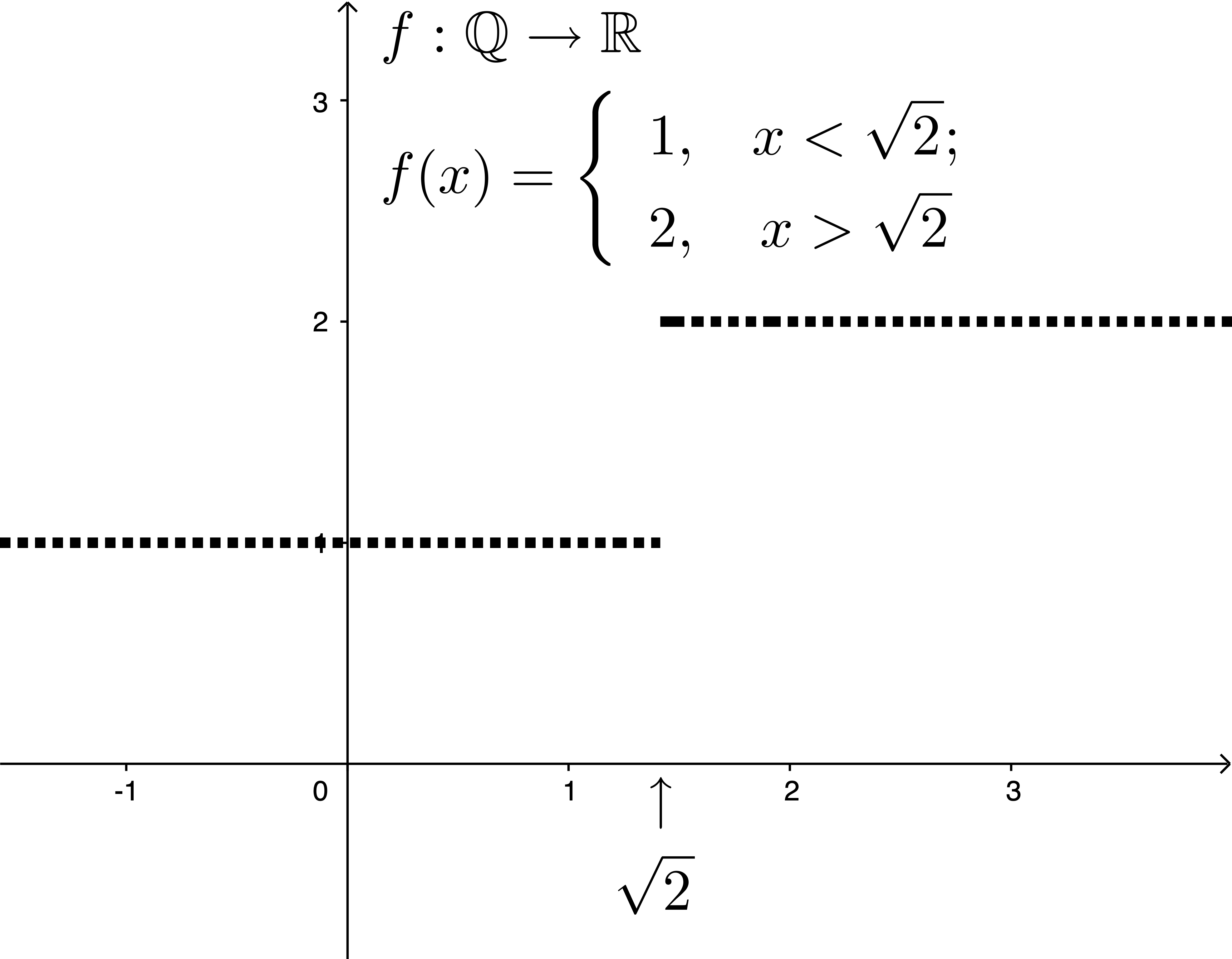
Example A

|
Claim: $f$ is continuous on $\Q$.
Discussion: Let $r\in \Q$.
Then $r\neq \sqrt{2}$.
So the number
\[
\delta = \abs{\sqrt{2}-r}\;\text{ is positive.}
\]
This means that the interval $(r-\delta, r+\delta)$ lies
either completely to the left or completely
to the right of $\sqrt{2}$.
$$|\,f(x)-f(r)| = 0 \lt \epsilon.$$ |
To be continuous or not to be?🧐
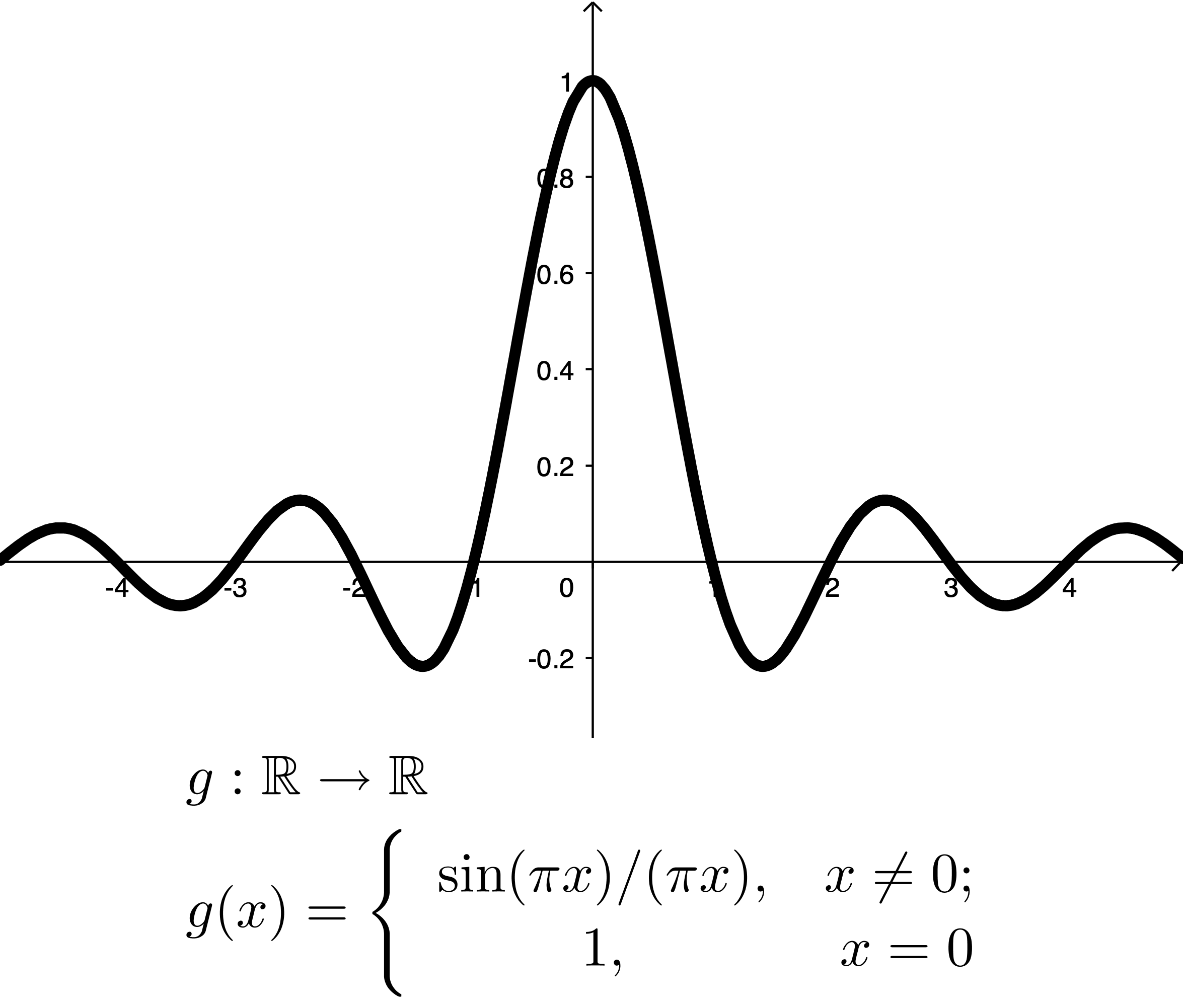
Example B

|
Claim: $g$ is continuous on $\R$.
Discussion:
In general we know that
\[
\lim_{z\ra 0} \frac{\sin (z)}{z}= 1.
\]
Since
$\displaystyle\lim_{x\ra 0} \frac{\sin(\pi x)}{\pi x}=1$
and $g(x) = 1$ for
$x=0,$ then $g$ is continuous on $\R$.
|
To be continuous or not to be? 🧐
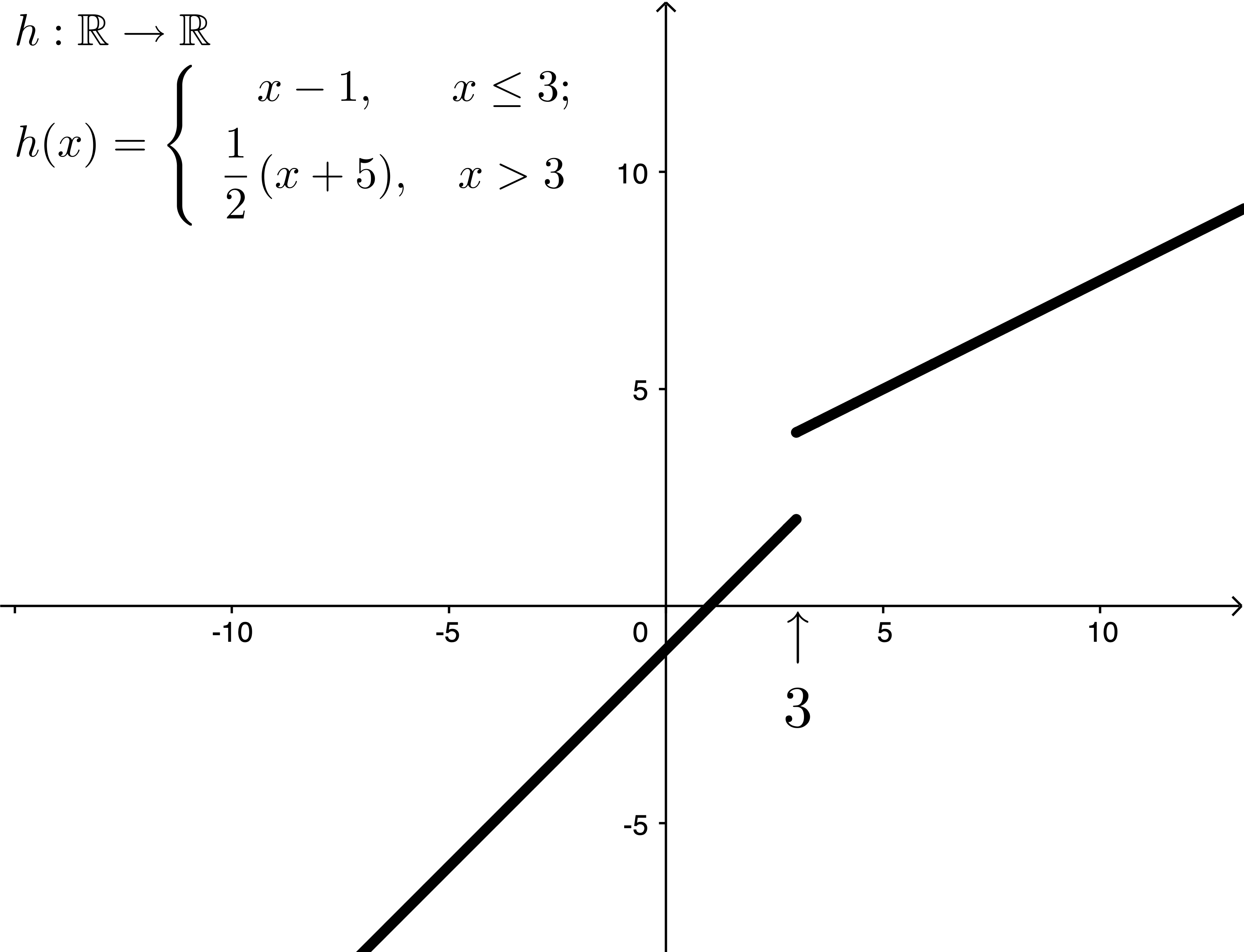
Example C

|
Claim: $h$ is NOT continuous at $x=3$.
Discussion:
Calculate the one-sided limits at $x=3$.
|