Problem Solving Techniques

In 1945 George Polya published the book How To Solve It which quickly became his most prized publication. It sold over one million copies and has been translated into 17 languages.

In this book he identifies four basic principles of problem solving.




Problem Solving Techniques

  • First Principle: Understand the problem
  • Second Principle: Devise a plan
  • Third Principle: Carry out the plan
  • Fourth Principle: Look back

Source: How To Solve It, by George Polya, 2nd ed., Princeton University Press, 1957.


The beauty of mathematics shows itself to patient followers.

Maryam Mirzakhani





The beauty of mathematics shows itself to patient followers.

Maryam Mirzakhani












Calculus &
Linear Algebra II

Review

Multiple integrals

1. Fubini's theorem

If $f(x,y)$ is integrable on the rectangle \[ R = \left\{ (x,y)~|~a\leq x\leq b, c\leq y\leq d \right\}, \] then

$\displaystyle \iint_R f(x,y)~ dA = \int_a^b \int_c^d f(x,y) ~dy~dx$

$\displaystyle \qquad \qquad \;\;\;= \int_c^d \int_a^b f(x,y) ~dx~dy$



Multiple integrals

1. Fubini's theorem


Multiple integrals

  1. Fubini's Theorem
  2. Double integrals $\iint f \,dA$ & Tripple integrals $\iiint f \,dV$
  3. Applications: Mass, Centroids, Moments and Moments of Inertia, etc.
  4. Basic transformations: Polar, Cylindrical, and Spherical

Multiple integrals

  1. Basic transformations: Polar, Cylindrical, and Spherical

$x=r\cos\theta,\\ y =r\sin \theta$

$x=r\cos\theta, \\y =r\sin \theta, \\z=z$

$x=r\cos\theta \sin \phi,\\ y =r\sin \theta\sin\phi, \\z = r \cos \phi$

Vector Calculus

Main results
  • $\displaystyle \int_a^b F'(x)\,dx =F(b)-F(a)$
  • $\displaystyle \int\limits_C \nabla f \pd d\r =f\left(\r(b)\right)-f\left(\r(a)\right)$
  • $\displaystyle \iint\limits_D\left( \frac{\partial F_2}{\partial x}- \frac{\partial F_1}{\partial y} \right) \,dA = \int\limits_C F_1\, dx + F_2 \,dy$
  • $\displaystyle \iint\limits_D \div \F \, dA = \int\limits_S \F \pd \n\, dS $
  • $\displaystyle \iiint\limits_E \div \F \, dV = \iint\limits_S \F \pd \n\, dS $
  • $\displaystyle \iint\limits_S \curl \F \pd \n~ dS = \int\limits_C \F \pd d\r$

Vector Calculus

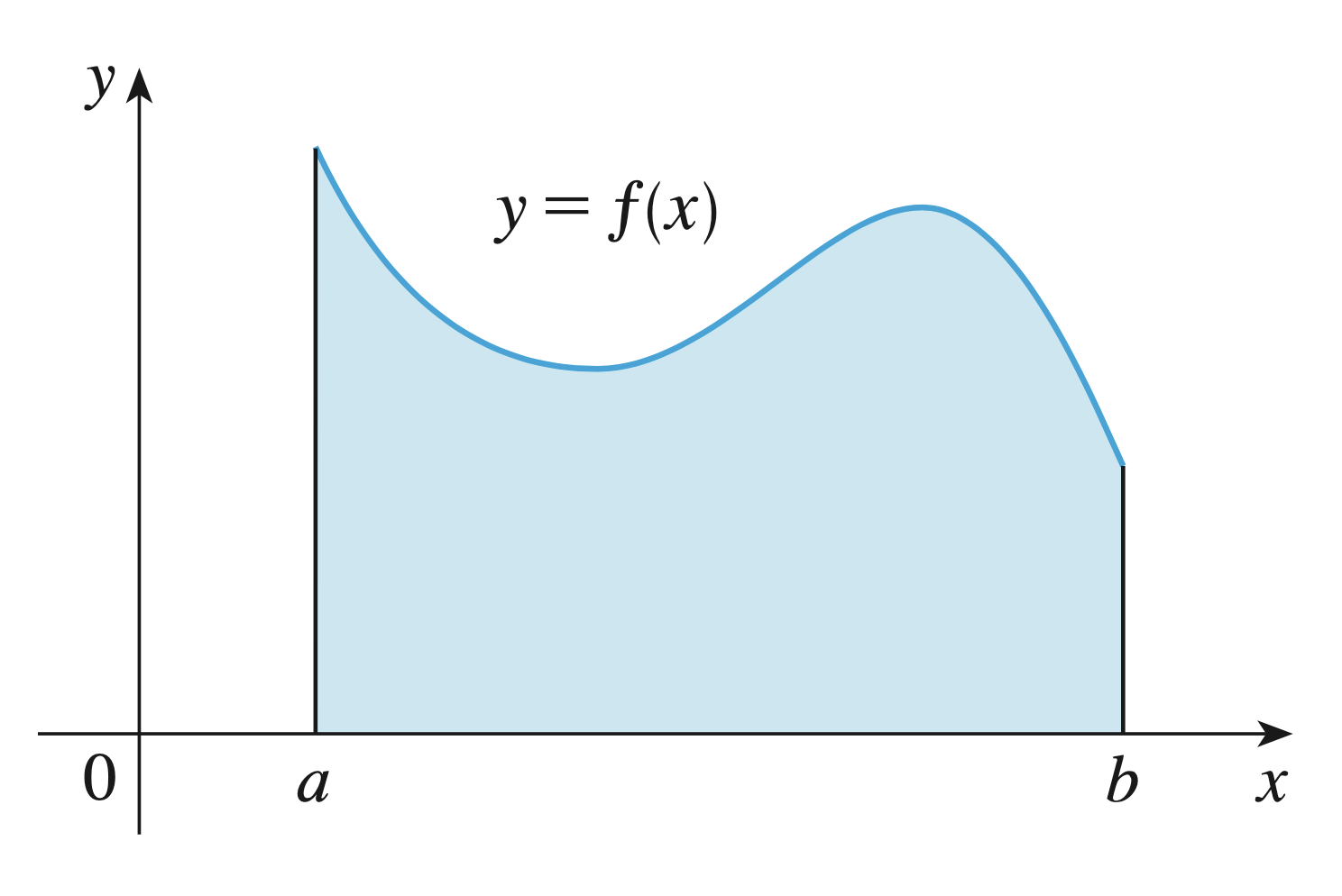
Fundamental Theorem of Calculus

\[ \int_a^b F'(x)\,dx =F(b)-F(a) \]



Vector Calculus

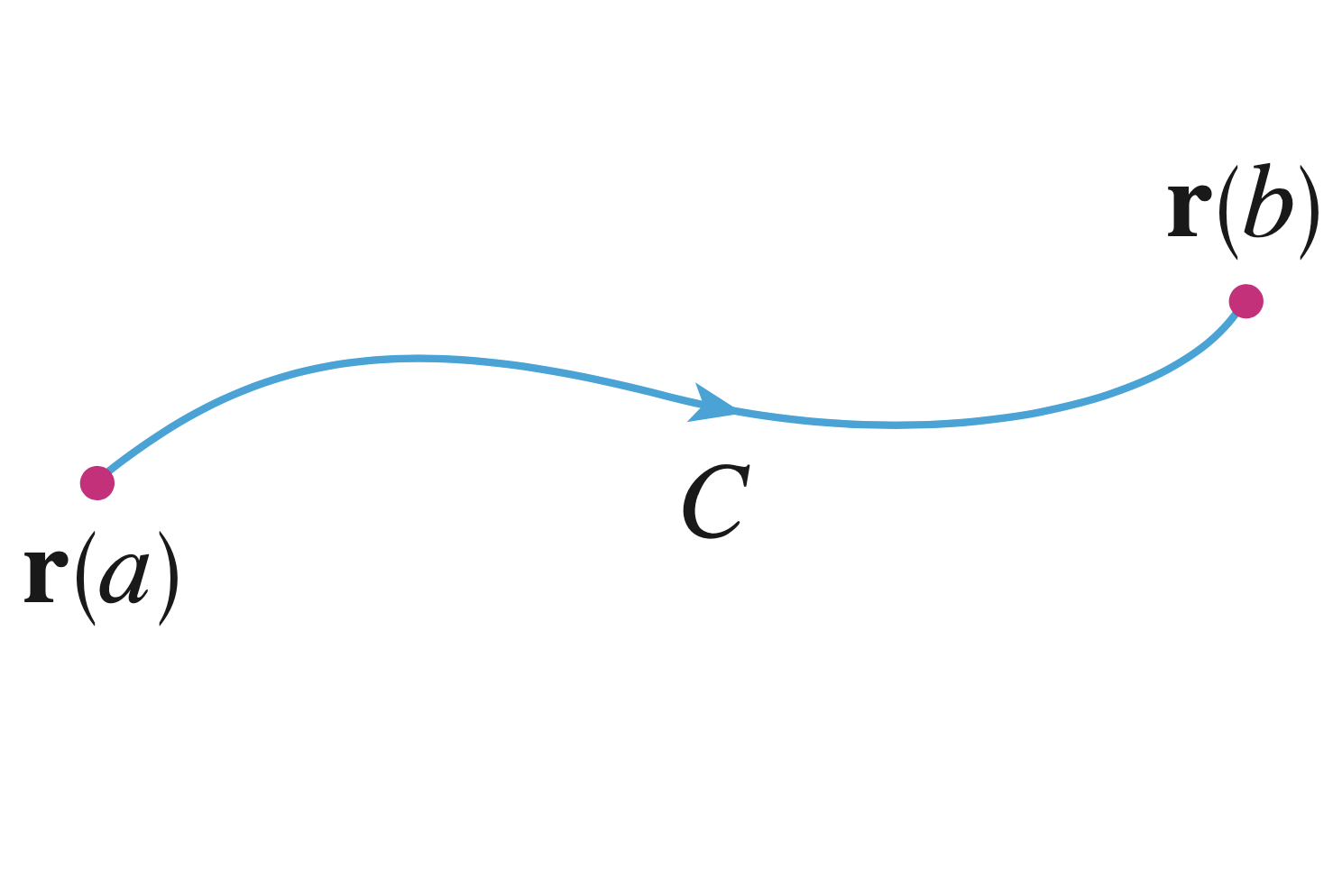
Fundamental Theorem for Line Integrals

\[ \int\limits_C \nabla f \pd d\r =f\left(\r(b)\right)-f\left(\r(a)\right) \]



Vector Calculus

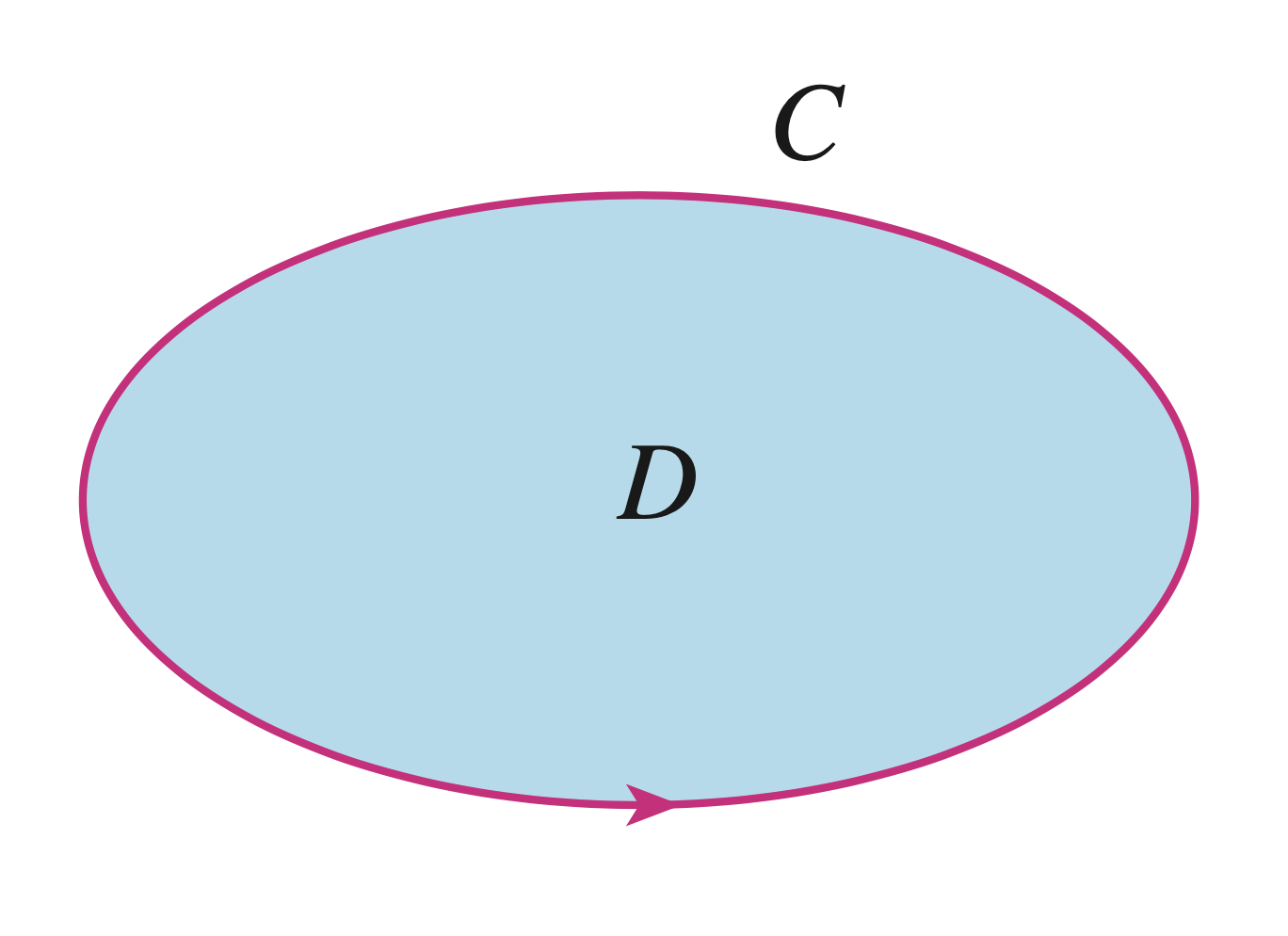
Green's Theorem

\[ \iint\limits_D\left( \frac{\partial F_2}{\partial x}- \frac{\partial F_1}{\partial y} \right) \,dA = \int\limits_C F_1\, dx + F_2 \,dy \]



Vector Calculus

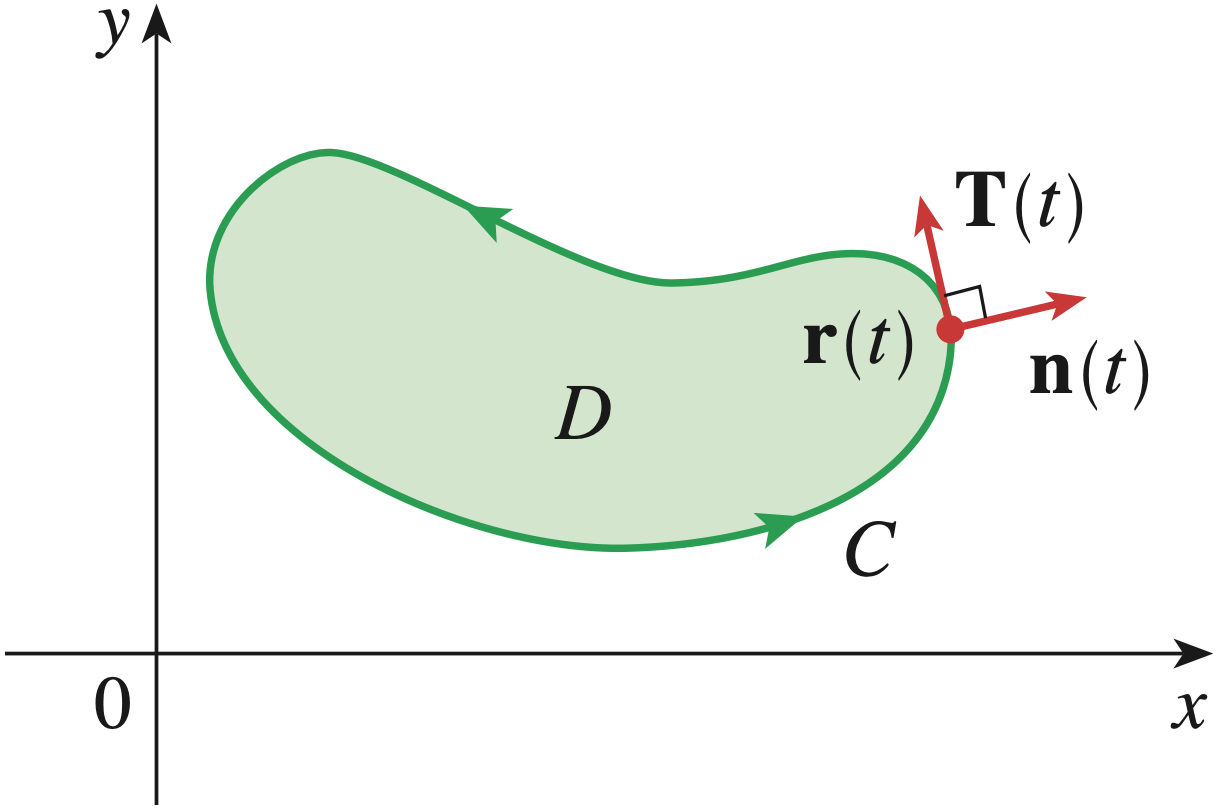
Gauss' Divergence Theorem in 2D

\[ \iint\limits_D \div \F \, dA = \int\limits_S \F \pd \n\, dS \]



Vector Calculus

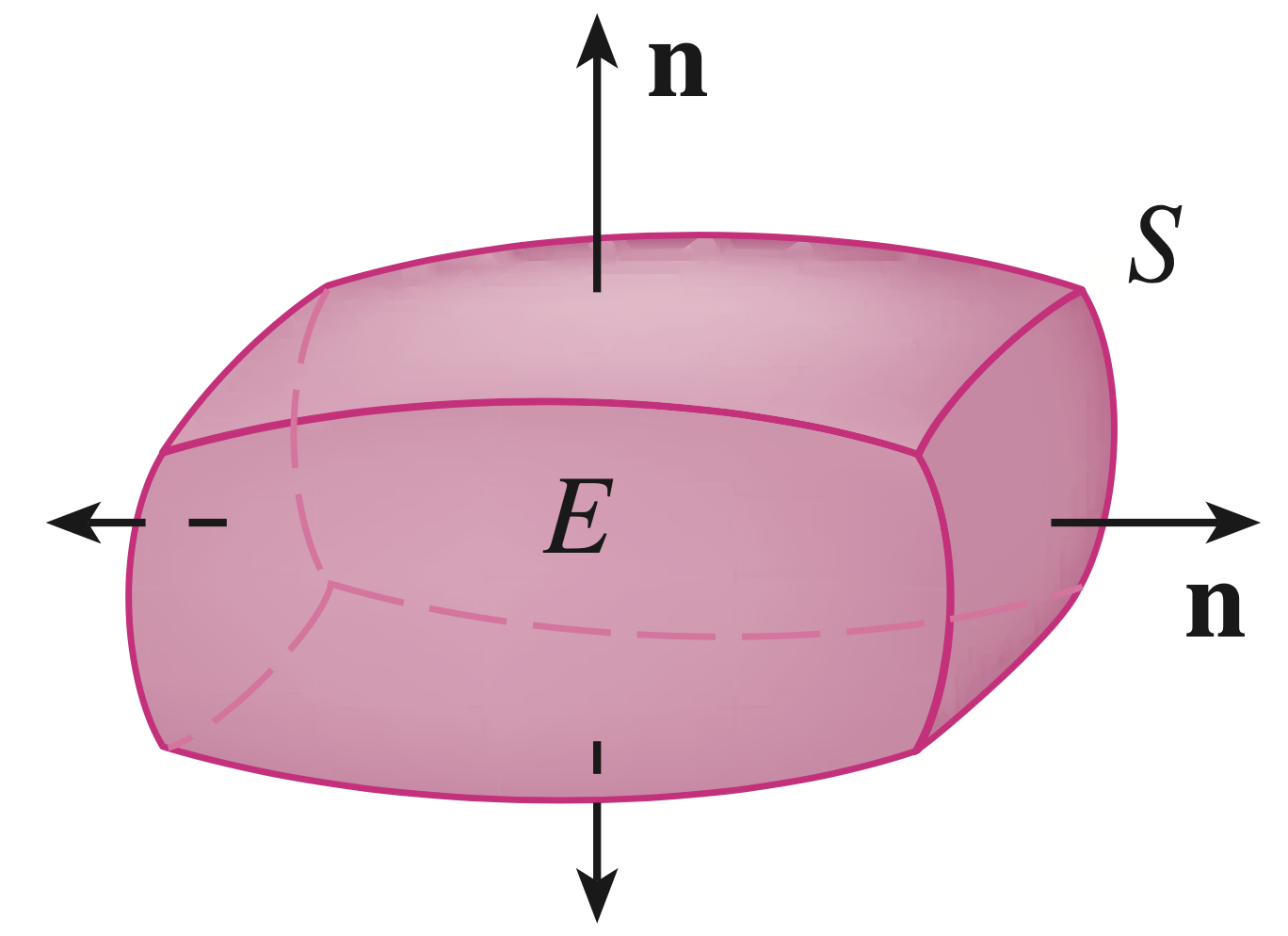
Gauss' Divergence Theorem in 3D

\[ \iiint\limits_E \div \F \, dV = \iint\limits_S \F \pd \n\, dS \]



Vector Calculus

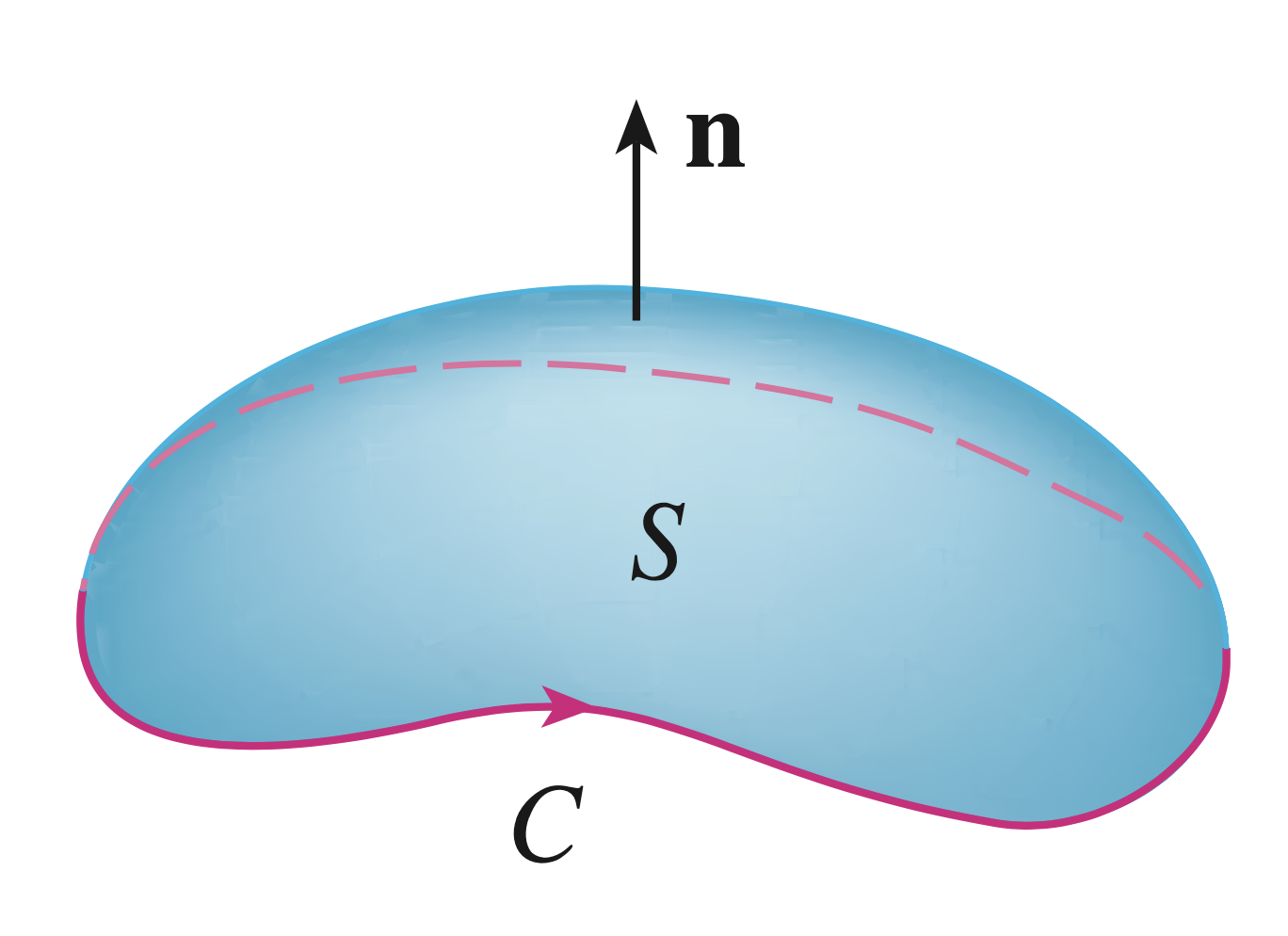
Stokes's Theorem

\[ \iint\limits_S \curl \F \pd \n ~dS = \int\limits_C \F \pd d\r \]



Vector Calculus

\[ \begin{array}{l} \displaystyle \int_a^b F'(x)\,dx = F(b)-F(a)\\ \displaystyle \int\limits_C \nabla f \pd d\r =f\left(\r(b)\right)-f\left(\r(a)\right)\\ \displaystyle \iint\limits_D\left( \frac{\partial F_2}{\partial x}- \frac{\partial F_1}{\partial y} \right) \,dA = \int\limits_C F_1\, dx + F_2 \,dy\\ \displaystyle \iint\limits_D \div \F \, dA = \int\limits_S \F \pd \n\, dS\\ \displaystyle \iiint\limits_E \div \F \, dV = \iint\limits_S \F \pd \n\, dS\\ \displaystyle \iint\limits_S \curl \F \pd \n~ dS = \int\limits_C \F \pd d\r\\ \end{array} \]


Vector Calculus

We can extend these results to higher dimensions

$ \ds \int_{\partial \Omega} \omega $ $ \ds= \int_{\Omega}d\omega $

$ \ds \int_{\partial \Omega} \omega $ $ \ds= \int_{\Omega}d\omega $


The integral of some differential form of dimension $k-1$,
over the boundary of some orientable manifold of dimension $k$,
is equal to the integral of its exterior derivative
over the whole of that orientable manifold.




Vector Calculus

We can extend these results to higher dimensions

$ \ds \int_{\partial \Omega} \omega $ $ \ds= \int_{\Omega}d\omega $


The integral of some differential form of dimension $k-1$,
over the boundary of some orientable manifold of dimension $k$,
is equal to the integral of its exterior derivative
over the whole of that orientable manifold.




Credits

Design, Images & Applets
Juan Carlos Ponce Campuzano