41.1 Area of a parametric surface

41.1 Area of a parametric surface

41.1 Area of a parametric surface

1. A partition of $S$ into patches will correspond to a partition of $D$ (in the $u$-$v$ plane) into small rectangles.

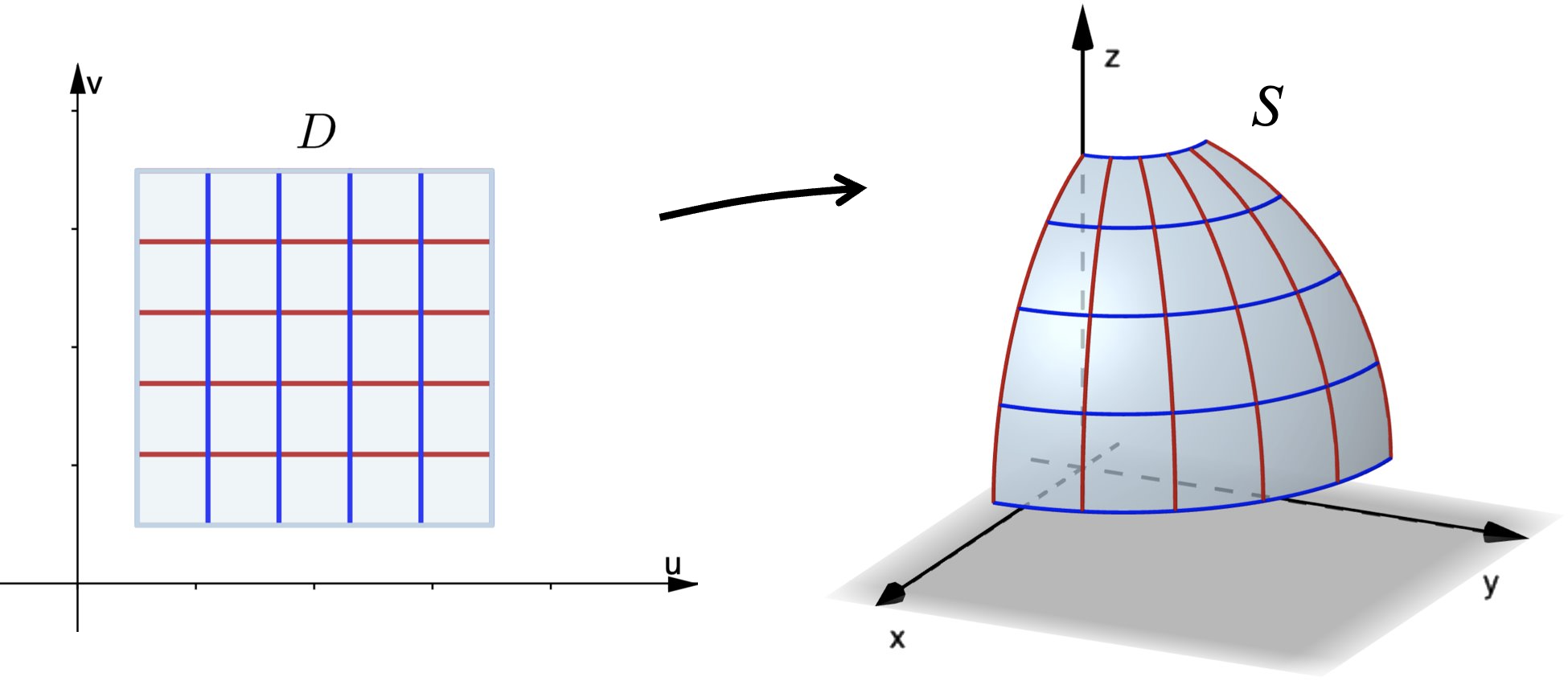
The dimensions of the rectangles in $D$ will be $\Delta u\Delta v$.

41.1 Area of a parametric surface

2. Let one of the edges of a single patch be defined from parameter values $(u, v)$ to $(u+ \Delta u, v)$.

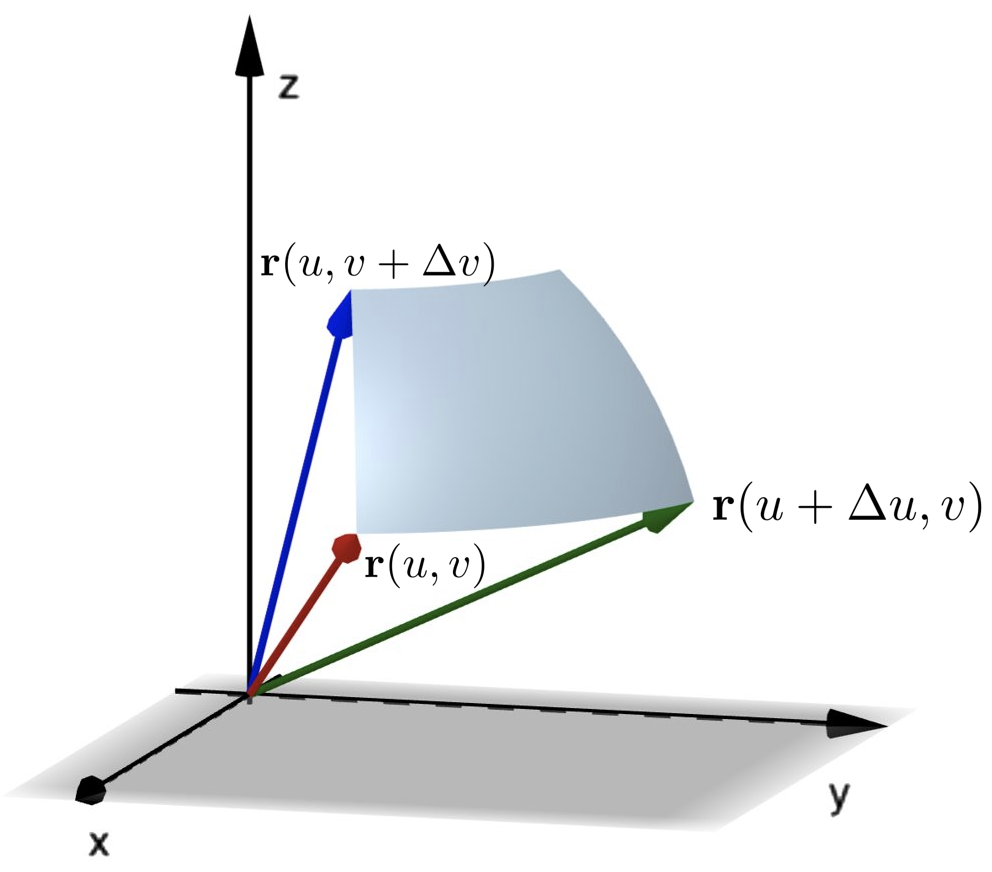
41.1 Area of a parametric surface

Using Pythagoras' law in three dimensions, we can approximate the length of this edge as $\text{length}$ $\approx \sqrt{\left(\Delta x\right)^2 + \left(\Delta y\right)^2 + \left(\Delta z\right)^2}$ $\displaystyle = \left(\sqrt{\left(\frac{\Delta x}{\Delta u}\right)^2 + \left(\frac{\Delta y}{\Delta u}\right)^2 + \left(\frac{\Delta z}{\Delta u}\right)^2} \right) \Delta u$ $\approx \norm{\r_u}\Delta u,$ where in this case we have used $$\Delta x = x(u + \Delta u, v) -x(u, v)$$ etc (i.e., the change is only in $u$). Similarly, for an edge of patch running from parameter values $(u, v)$ to $(u, v + \Delta v)$ the length of that edge will be approximately $||\r_v||\Delta v.$

41.1 Area of a parametric surface

At the corner of the patch corresponding to parameter values $(u, v),$ we can define the two vectors $\r_u\Delta u$ and $\r_v\Delta v$ which form two sides of a parallelogram, the side lengths of which coincide with our approximations to the lengths of the edges of the patch.

41.1 Area of a parametric surface

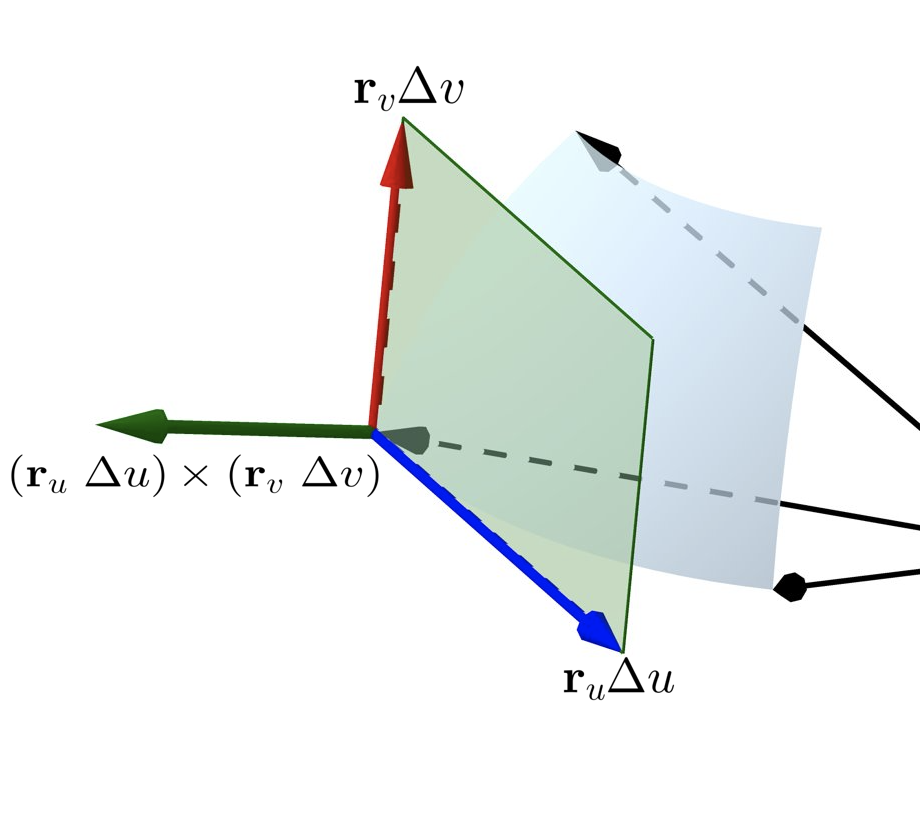
The vector $\left(\r_u~\Delta u\right) \times \left(\r_v~\Delta v\right)$ is normal to the surface (and hence the tangent plane) at that point. Its magnitude gives the area of the parallelogram we use to approximate the area of the patch $\Delta S$. We then have \[ \Delta S \approx \norm{\r_u \times \r_v} ~\Delta u ~\Delta v. \] Adding these approximations for each patch in $S$ gives us an approximation to the area of $S$: area of $S$ $\displaystyle\approx \sum _i \Delta S_i$ $\displaystyle= \sum_i \norm{\r_{u_i} \times \r_{v_i}} ~\Delta u_i ~\Delta v_i.$

41.1 Area of a parametric surface

4. Finally taking the limit as $\Delta u, \Delta v \to 0$ we obtain \[ \text{surface area} = \iint_S dS = \iint_D \norm{\r_u \times \r_v} ~du ~dv. \]

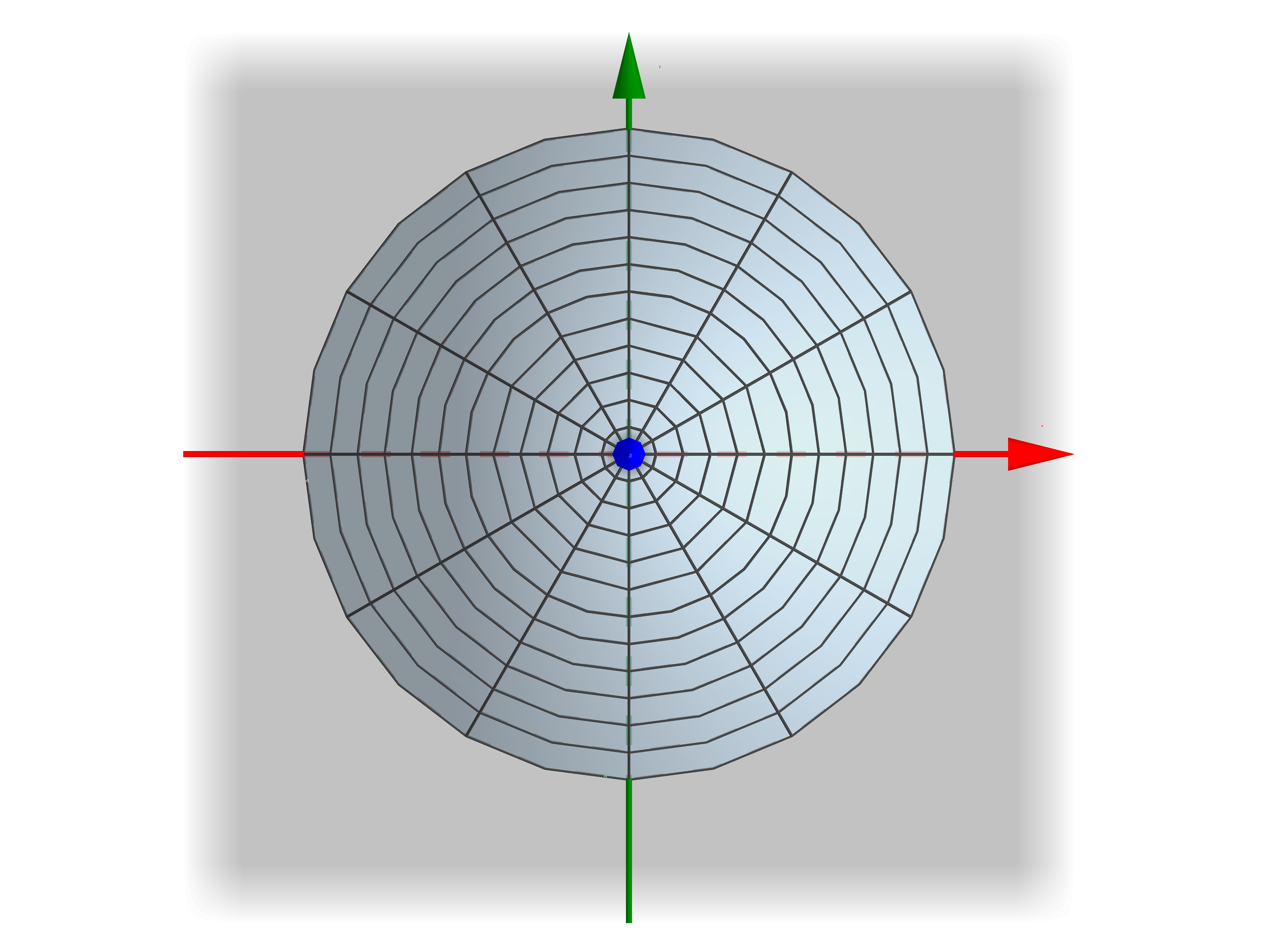
41.1.1 Application: find the surface area of the paraboloid $z=1-x^2-y^2$ for $z\geq 0 $

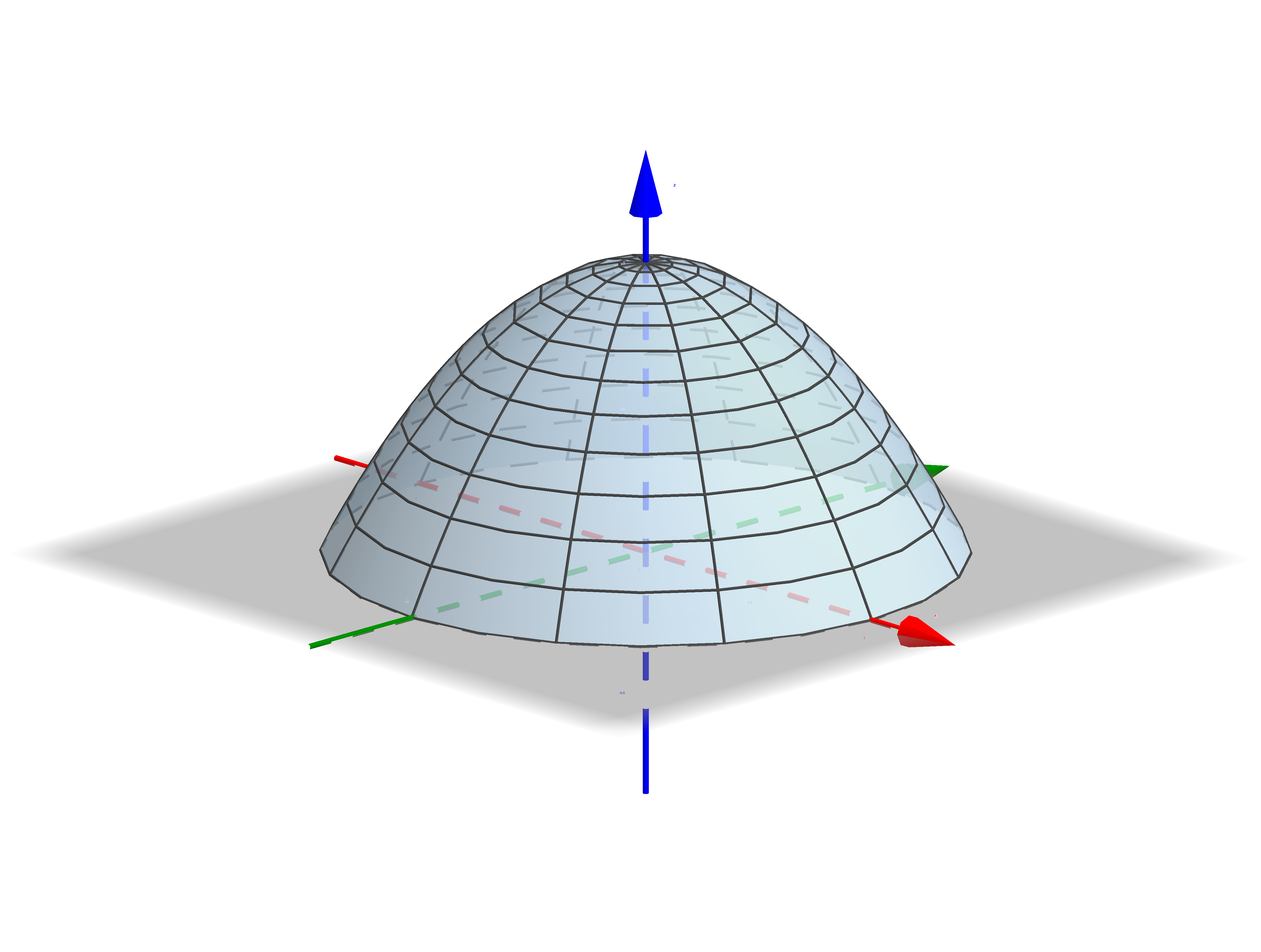
41.1.1 Application: find the surface area of the paraboloid $z=1-x^2-y^2$ for $z\geq 0 $

Let's begin with the parametrisation of $S$. Consider $x$ and $y$ as parameters, so \[ \r(x,y) = x~\i + y~\j + \left(1-x^2-y^2\right)~\k \] $x$ and $y$ are bounded by intersection curve of \[ z=1-x^2-y^2\quad \text{and} \quad z=0. \] That is, $x^2+y^2=1$. So the domain for $x$ and $y$ is given by $x^2+y^2\leq 1$.

41.1.1 Application: find the surface area of the paraboloid $z=1-x^2-y^2$ for $z\geq 0 $

Thus \[ \r_x = \i-2x~\k, \quad \r_y = \j-2y~\k, \] and $ \r_x\times\r_y = \left| \begin{array}{ccc} \i & \j & \k\\ 1 & 0 & -2x \\ 0 & 1 & -2 y \end{array} \right| $ $= 2x~\i + 2y ~\j + \k$. Since $||\r_x\times\r_y||=\sqrt{4x^2+4y^2+1},$ then \[ dS = ||\r_x\times\r_y|| ~dx~dy = \sqrt{4x^2+4y^2+1}~dx~dy. \]

41.1.1 Application: find the surface area of the paraboloid $z=1-x^2-y^2$ for $z\geq 0 $

$\Rightarrow \text{Area}$ $\displaystyle = \iint_S dS$ $\displaystyle = \iint\limits_{x^2+y^2\leq 1} ||\r_x\times\r_y|| ~dx~dy$ $\displaystyle = \iint\limits_{x^2+y^2\leq 1} \sqrt{4x^2+4y^2+1}~dx~dy$ $\displaystyle = \int_0^{2\pi} \int_0^1 \sqrt{4r^2+1}~r~dr~d\theta$ $\displaystyle = \int_0^{2\pi} \left[ \bigg. \frac{1}{8}~\frac{2}{3} \left(4r^2+1\right)^{3/2} \bigg|_0^1 \right] d\theta$ $\displaystyle = \int_0^{2\pi} \left[ \frac{5 \sqrt{5} -1}{12} \right] d\theta$ $\displaystyle =\frac{\pi}{6} \left(5 \sqrt{5} - 1\right).$

41.2 More on calculating surface integrals, applications

41.2 More on calculating surface integrals, applications

41.2 More on calculating surface integrals, applications

41.2 More on calculating surface integrals, applications

41.2 More on calculating surface integrals, applications

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

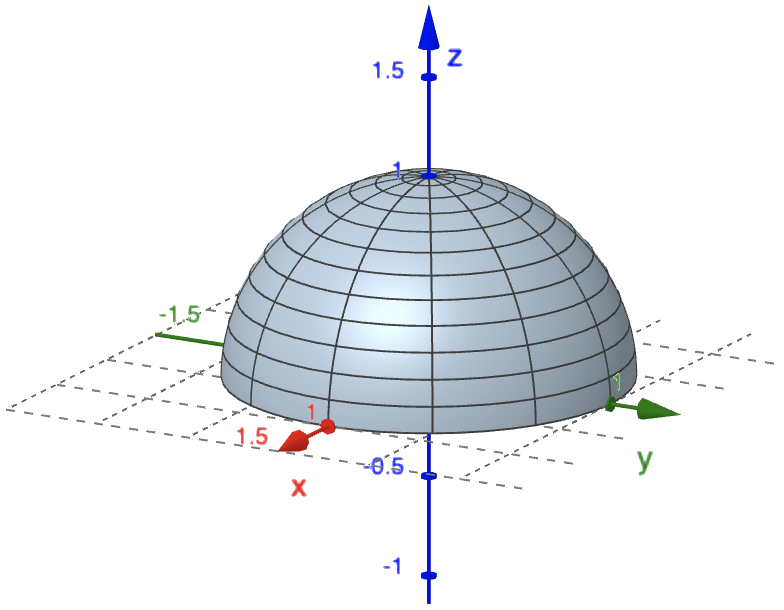
Here we have that $ \displaystyle \text{Average temp.} = \frac{\displaystyle\iint_S T~dS}{\text{area of }S}\qquad \qquad \qquad \qquad $ $\qquad \;\;= \frac{\displaystyle\iint_{S_1} T~dS + \iint_{S_2} T~dS }{\displaystyle\iint_{S_1} ~dS + \iint_{S_2} ~dS },$ where $S_1$ is the base and $S_2$ is the top.

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

For $S_1$: Here we have a disk in the $xy$-plane of radius $1$. Then the parametrisation is \[ \r(x,y) = x~\i+y~\j+0~\k\quad (x^2+y^2\leq 1). \] Then $\r_x = \i$, $\r_y = \j$ and \[ dS = \norm{\r_x\times \r_y }~dx~dy= dx~dy. \] So $\displaystyle \iint_{S_1} T~dS = \iint_{S_1} \left( x^2+y^2+z^2+4\right)dx~dy$ or $\displaystyle \iint_{S_1} T~dS = \iint_{S_1} \left( x^2+y^2+(0)^2+4\right)dx~dy$ That is $\displaystyle \iint_{S_1} T~dS = \iint_\limits{x^2+y^2\leq 1} \left( x^2+y^2+4\right)dx~dy$.

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

For $S_1$: Using polar coordinates \[ x = r\cos\theta , \quad y = r \sin \theta \] with $0\leq r \leq 1$ and $0\leq \theta \leq 2 \pi$, we have $\displaystyle \iint_{S_1} T~dS $ $\displaystyle = \iint_\limits{x^2+y^2\leq 1} \left( x^2+y^2+4\right)dx~dy$ $\displaystyle = \int_0^1 \int_0^{2\pi} \left(r^2 \cos ^2 \theta + r^2 \sin^2 \theta + 4\right)r ~dr~d\theta $ $\displaystyle = \int_0^1 \int_0^{2\pi} \left(r^2 + 4\right)r ~dr~d\theta $ $\displaystyle = \frac{9 \pi}{2}$

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

For $S_1$: Using polar coordinates \[ x = r\cos\theta , \quad y = r \sin \theta \] with $0\leq r \leq 1$ and $0\leq \theta \leq 2 \pi$, we have $\displaystyle \iint_{S_1} T~dS $ $\displaystyle = \frac{9 \pi}{2}$. Finally $\;\;\displaystyle \iint_{S_1}~dS $ $\displaystyle = \text{Area of the disk of radius 1}$ $=\pi (1)^2$ $= \pi$.

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

For $S_2$: Now we have a half sphere of radius 1. Then the parametrisation is \[ \r(\theta,\phi ) = \cos\theta \sin \phi~\i+ \sin\theta \sin \phi ~\j+\cos \phi~\k \] where $0\leq \theta \leq 2 \pi$ and $0 \leq \phi \leq \pi/2$. Then $ \quad \r_{\theta} = -\sin\theta \sin \phi~\i+ \cos\theta \cos \phi ~\j+0~\k $ $ \quad \r_{\phi} = \cos\theta \cos \phi~\i+ \sin\theta \cos \phi ~\j- \sin \phi~\k $

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

$\norm{\r_{\theta}\times\r_{\phi} } $ $=\sqrt{ \cos^2 \theta \sin ^4 \phi + \sin^2 \theta \sin ^4 \phi + \sin^2 \phi \cos^2 \phi }$ $ =\sqrt{ \left( \cos^2 \theta + \sin^2 \theta \right) \sin ^4 \phi + \sin^2 \phi \left(1- \sin ^2\phi\right) }$ $=\sqrt{ \sin^4 \phi + \sin^2 \phi - \sin^4\phi }$ $ =\sqrt{ \sin^2 \phi }$ $= \sin \phi$ So \[ \iint_{S_2} T~dS = \iint_{S_2}\left(x^2+y^2+z^2+4\right)dS \]

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

$\displaystyle \iint_{S_2} T~dS $ $\displaystyle = \iint_{S_2}\left(x^2+y^2+z^2+4\right)dS$ $ \displaystyle = \iint_{S_2}\left(1+4\right)dS$ $ \displaystyle = 5 \iint_{S_2}dS$ $\displaystyle = 5 \left(\text{Surface area of the half sphere}\right)$ $ =\displaystyle 5\left(\frac{1}{2}\right) \left(4 \pi \right)\left(1 \right)^2$ $= 10 \pi.$ And $\displaystyle \iint_{S_2} ~dS $ $\displaystyle = \text{Surface area of the half sphere}$ $=$ $ \displaystyle\, 2 \pi$.

41.2.1 The function $T (x, y, z) = x^2 + y^2 + z^2 + 4 $

gives the temperature at any point $(x, y, z)$ on the surface of a solid hemisphere of radius 1 centred at the origin, defined for $z\geq 0$. Find the average temperature over the surface

Therefore $ \displaystyle \text{Average temp.} = \frac{\displaystyle\iint_{S_1} T~dS + \iint_{S_2} T~dS }{\displaystyle\iint_{S_1} ~dS + \iint_{S_2} ~dS }$ $\;\;\;\quad \displaystyle = \frac{\displaystyle \frac{9\pi}{2}+ 10 \pi}{\displaystyle \pi + 2\pi}$ $\displaystyle = \frac{29}{6}\;$.