Calculus &
Linear Algebra II
Chapter 35
35 The fundamental theorem for line integrals, path independence
By the end of this section, you should be able to answer the following questions:
- How do you evaluate line integrals?
- What is the fundamental theorem for line integrals and its consequences?
- What is a path independent line integral and what are its connections with conservative vector fields and line integrals over closed curves?
35.1 Line integrals in the plane
Recall the definite integral $\displaystyle \int_a^b f(x) ~dx$ gives the net area above the $x$-axis and below the curve $y=f(x).$ We can generalise this.
Consider the following problem:
How do we calculate the area of the region between
the curve $C$ in the $x$-$y$ plane and its image on the surface $z = f(x,y)$?
35.1 Line integrals in the plane
35.1 Line integrals in the plane
Divide $C$ into small arcs of length $\Delta S$. This divide the area into strips of base length $\Delta S$ and height $f(x^*,y^*),$ where $(x^*, y^*)$ is a representative point in an arc. Then \[ \text{the area in question} = \int_C f(x,y)~ dS, \] where $dS$ is the infinitesimal element of arclength of $C.$ If the curve $C$ can be parametrised by $\r(t) = x(t)~\i + y(t) ~\j\;$ for $a\leq t\leq b,$ then $dS = ||\r'(t)||dt$, and the area can be expressed by the formula \[ \text{area} = \int_C f(x,y)~ dS = \int_a^b f\left(x(t),y(t)\right)||\r'(t)||~dt. \]
35.2 Work done by a force, line integrals
of vector fields
We can also consider integrating a vector field over a curve in the plane.
In the case $\F$ is a field of force you should already have an idea (from MATH1052/1072) how to determine the work done by $\F$ in moving a particle along a curve $C$. First recall
- Constant $F$ in 1D over a distance $d$, the work done is given by $W = F d$.
- Constant $\F$ in 2D over a straight line between points $P$ and $Q$, $W=\F\pd \overrightarrow{PQ}.$
35.2 Work done by a force, line integrals
of vector fields
We can use these straightforward cases to derive the more general expression for work done by a variable force $F(x,y)$ over a piecewise continuous smooth curve $C$: \[ W = \int_C \F(x,y)\pd \T(x,y)~dS \] where $\T (x, y)$ is a unit tangent vector to $C$ at a given point $(x, y)$ on $C$.
35.2 Work done by a force, line integrals
of vector fields

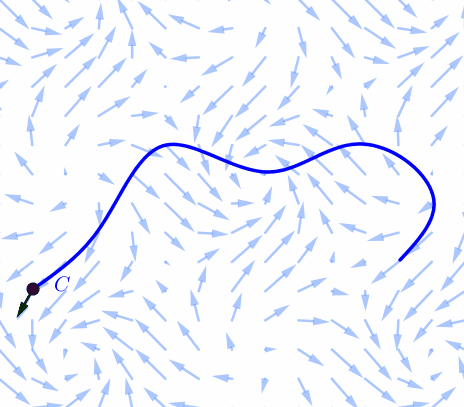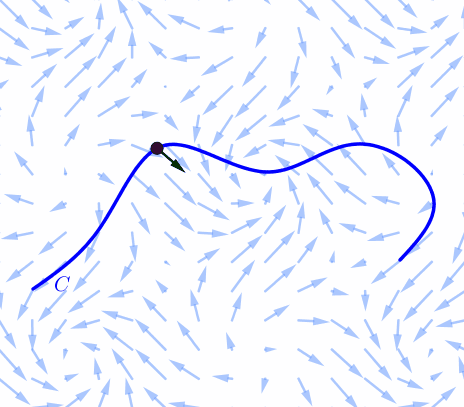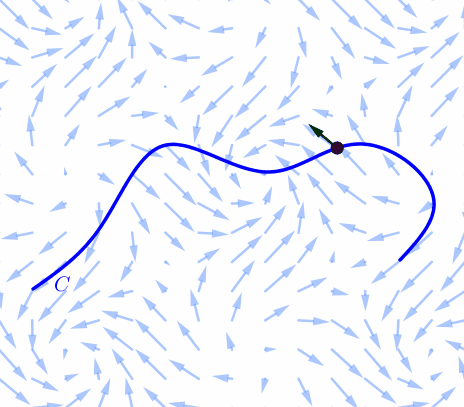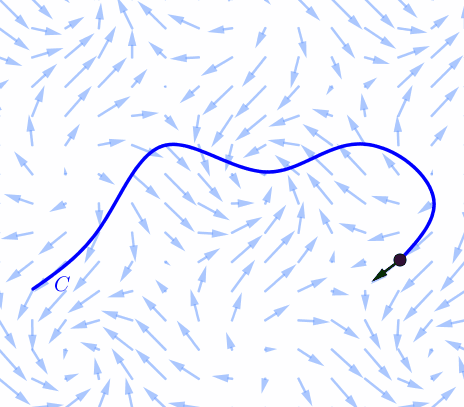

|
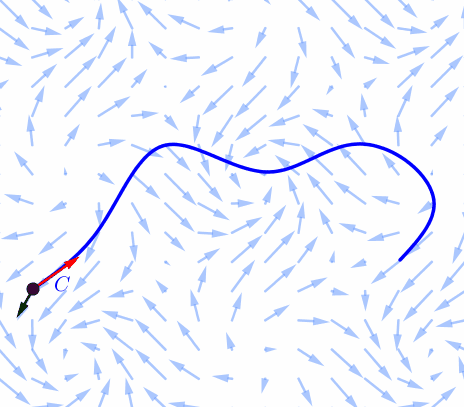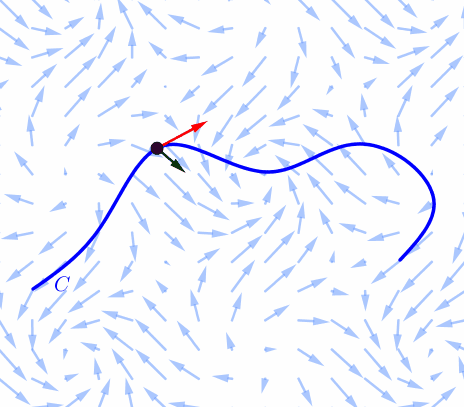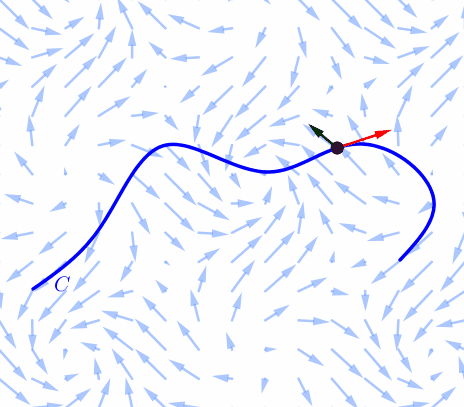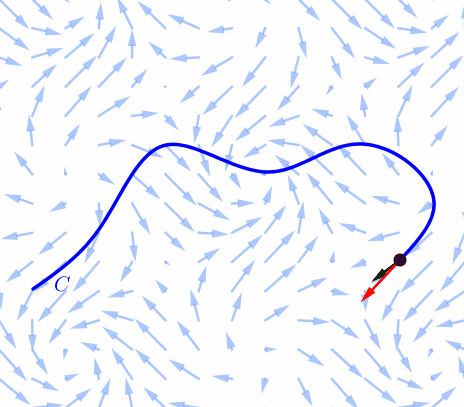
Consider a force field $\F(x,y)$ and a piecewiese continuous smooth curve $C.$ We wish to compute the work done by this force in moving a particle along a smooth curve $C.$ We divide $C$ into subarcs $P_{i-1}$-$P_i$ with lengths $\Delta S_i$ by dividing the parameter interval $[a, b]$ into subintervals of equal width. |
35.2 Work done by a force, line integrals
of vector fields
|
|
Choose a point $P_i^*$ on the $i$th subarc corresponding to the parameter value $t_i^*.$ If $\Delta S_i$ is small, then as the particle moves from $P_{i-1}$ to $P_i$ along the curve, it proceeds approximately in the direction of $\T(t_i^*),$ the unit tangent vector at $P_i^*.$ Thus the work done by the force $\F$ in moving the particle from $P_{i-1}$ to $P_i$ is approximately \[ \F^* \pd \T^* \Delta S_i \] |
35.2 Work done by a force, line integrals
of vector fields
|
|
Thus the work done by the force $\F$ in moving the particle from $P_{i-1}$ to $P_i$ is approximately \[ \F^* \pd \T^* \Delta S_i \] and the total work done in moving the particle along $C$ is approximately \[ \sum_{i=1}^n \F^* \pd \T^* \Delta S_i \] |
35.2 Work done by a force, line integrals
of vector fields

|
Intuitively, we see that these approximations have to become better as $n\to \infty$ ($\Delta S_i\to 0$). Therefore we define the work $W$ done by the force field $\F$ as the limit of the Riemann sums in $\sum_{i=1}^n \F^* \pd \T^* \Delta S_i.$ That is \[ W = \int_C\F\pd \T~dS \] |
35.3 Common notation
Let $C$ be a piecewise continuous smooth curve in the $x$-$y$ plane connecting points $A$ and $B.$ Let $\,\F(x,y)= F_1(x,y)~\i + F_2(x,y)~\j\,$ be a vector field. The line integral $\int_C \F(x,y) \pd \T(x,y) ~dS$ is often expressed as \[ \int_C \F(\r)\pd d\r \quad \text{or}\quad \int_C F_1(x,y)dx+F_2(x,y)dy. \]
The expressions use the notation $\r = x~\i + y~\j,$ $d\r = dx~\i + dy~\j.$
Remark: In this notation,
\[
\text{work done by } \F \text{ along the curve } C: W = \int_C\F(\r)\pd d\r.
\]
35.3 Common notation
Need to prove $\displaystyle \int_C \F(x,y) \pd \T(x,y) ~dS = \int_C \F(\r)\pd d\r.$
Let $\r(t) =x(t)~\i+y(t)~\j$ be a parametrisation of the curve $C$ with $t\in[a,b].$ Then the unit tangent vector to $C$ is
$\displaystyle \T=\frac{\r'(t)}{\norm{\r'(t)}}\;\;$ and $\displaystyle\;\; dS = \norm{\r'(t)}dt$
Then
| $\displaystyle \int_C \F\pd \T ~dS $ | $\displaystyle = \int_a^b \F(\r) \pd \frac{\r'(t)}{\norm{\r'(t)}} \left(\norm{\r'(t)}dt\right) $ $\displaystyle = \int_a^b \F(\r) \pd \r'(t)~dt $ |
| $\displaystyle = \int_C \F(\r) \pd d\r $ $\displaystyle = \int_C F_1(x,y)~dx+F_2(x,y)~dy.$ |
35.4 Evaluating line integrals of vector fields
To evaluate $\displaystyle \int_C\F(\r)\pd d\r$ the strategy is to parameterise $C$ and express all quantities in the line integral in terms of this parameterisation. Namely
- Parameterise $C$ by specifiying a vector function $\r(t) = x(t)~\i + y(t)~\j$ with $t \in [a, b]$ that describes $C.$
- Write $\F (\r)$ restricted to $C$ as $\F (\r(t)) = \F (x(t), y(t)).$
- Write $d\r=\r'(t)~dt.$
- Convert the line integral into an ordinary integral in terms of the parameter $t$: \[ \int_C\F(\r)\pd d\r = \int_a^b \F(\r(t))\pd \r'(t)~dt. \]
35.4.1 Example: Evaluate
$\displaystyle \int_C \left( \left(x^2-y \right)dx + \left(y^2+x \right)dy \right) $ along the curve $C$ given by: (i) the straight line from $A$ to $B$; (ii) the parabola $y=x^2+1$ from $A$ to $B$. Here $A= (0,1)$, $B=(1,2)$.
35.4.1 Example: Evaluate
$\displaystyle \int_C \left( \left(x^2-y \right)dx + \left(y^2+x \right)dy \right) \,$ along the curve $C$ given by: (i) the straight line from $A$ to $B$; (ii) the parabola $y=x^2+1$ from $A$ to $B.$ Here $A= (0,1),$ $B=(1,2).$
|
|
(i) First we parametrise the line from $A$ to $B$. This is the equation $y = x+1$. Then for $$C_1: \;(x=t, y = t+1).$$ So we have \[ \r(t) = x(t) ~\i + y(t)~\j =t~\i+ (t+1)~\j \] for $0\leq t \leq 1$. Note that $\r(0)= A=(0,1)$ and $\r(1) = B = (1,2)$. |
35.4.1 Example: Evaluate
$\displaystyle \int_C \left( \left(x^2-y \right)dx + \left(y^2+x \right)dy \right) \,$ along the curve $C$ given by: (i) the straight line from $A$ to $B$; (ii) the parabola $y=x^2+1$ from $A$ to $B.$ Here $A= (0,1),$ $B=(1,2).$
|
|
Parametrisation: $ \r(t) =t~\i+ (t+1)~\j $ for $0\leq t \leq 1$. Thus $$d\r = \r'(t)dt = (\i+ \j)~dt.$$
|
35.4.1 Example: Evaluate
$\displaystyle \int_C \left( \left(x^2-y \right)dx + \left(y^2+x \right)dy \right) \,$ along the curve $C$ given by: (i) the straight line from $A$ to $B$; (ii) the parabola $y=x^2+1$ from $A$ to $B.$ Here $A= (0,1),$ $B=(1,2).$
|
|
Now, since $\F\pd d\r=2\left(t^2+t\right)dt$, then
|
35.4.1 Example: Evaluate
$\displaystyle \int_C \left( \left(x^2-y \right)dx + \left(y^2+x \right)dy \right) \,$ along the curve $C$ given by: (i) the straight line from $A$ to $B$; (ii) the parabola $y=x^2+1$ from $A$ to $B.$ Here $A= (0,1),$ $B=(1,2).$
|
|
(ii) Now we need to parametrise the parabola from $A$ to $B$. This is the equation $y = x^2+1$. Then for $$C_2: \;(x=t, y = t^2+1).$$ So we have \[ \r(t) = x(t) ~\i + y(t)~\j =t~\i+ (t^2+1)~\j \] for $0\leq t \leq 1$. Note that $\r(0)= A=(0,1)$ and $\r(1) = B = (1,2)$. |
35.4.1 Example: Evaluate
$\displaystyle \int_C \left( \left(x^2-y \right)dx + \left(y^2+x \right)dy \right) \,$ along the curve $C$ given by: (i) the straight line from $A$ to $B$; (ii) the parabola $y=x^2+1$ from $A$ to $B.$ Here $A= (0,1),$ $B=(1,2).$
|
|
Parametrisation: $ \r(t) =t~\i+ (t^2+1)~\j $ for $\,0\leq t \leq 1.$ Thus $$d\r = \r'(t) dt= \left(\i+ 2t~\j\right)~dt.$$
|
35.4.1 Example: Evaluate
$\displaystyle \int_C \left( \left(x^2-y \right)dx + \left(y^2+x \right)dy \right) \,$ along the curve $C$ given by: (i) the straight line from $A$ to $B$; (ii) the parabola $y=x^2+1$ from $A$ to $B.$ Here $A= (0,1),$ $B=(1,2).$
|
|
Now, since $\F\pd d\r=\left[-1 + 2t \left((t^2+1)^2+t\right)\right]dt$, then
|
35.4.1 Example: Evaluate
$\displaystyle \int_C \left( \left(x^2-y \right)dx + \left(y^2+x \right)dy \right) \,$ along the curve $C$ given by: (i) the straight line from $A$ to $B$; (ii) the parabola $y=x^2+1$ from $A$ to $B.$ Here $A= (0,1),$ $B=(1,2).$
|
|
Note the line integrals in this example are path dependent. In other words, they have different values for different paths. \[ \int_{C_1} \F\pd d\r = \frac{5}{3} \;\; \text{and}\;\;\int_{C_2} \F\pd d\r = 2. \] We will now investigate path independent line integrals. |
35.5 Line integrals of conservative vector fields, path independence
If $\F$ is a continuous vector field with domain $D$, we say the line integral $\displaystyle \int_C \F\pd d\r$ is path independent if \[ \int_{C_1}\F\pd d\r = \int_{C_2}\F\pd d\r \] for any two paths $C_1$ and $C_2$ in $D$ that have the same end points.
35.5.1 The fundamental theorem for line integrals
If $C$ is a smooth curve determined by $\r(t)$ for $t \in [a,b]$ and $f(x,y)$ is differentiable with $\nabla f$ being continuous on $C,$ then \[ \int_C \nabla f\pd d\r = f\big(\r(b)\big)- f\big(\r(a)\big). \]
35.5.1 The fundamental theorem for line integrals
Proof: Recall that $\,\nabla f = \dfrac{\partial f}{\partial x}~\i + \dfrac{\partial f}{\partial y}~\j\,$ and consider the vector function $\r(t)$ with $a \leq t \leq b.$ So $d\r = \r'(t) dt.$ Then we have that
| $\displaystyle \int_C\nabla f\pd d\r$ | $\displaystyle =\int_{t=a}^{t=b} \nabla f \left(\r(t)\right)\pd \r'(t)~dt$ $\displaystyle =\int_{a}^{b} \left( \frac{\partial f}{\partial x} \frac{d x}{d t}+ \frac{\partial f}{\partial y} \frac{dy}{d t} \right)dt$ |
| $\displaystyle =\int_{a}^{b} \frac{d}{dt}~f\left(\r(t)\right) dt$ | |
| $\displaystyle = f\big(\r(b)\big)- f\big(\r(a)\big).$ |
The last step follows from the Fundamental Theorem of Calculus. $\blacksquare$
35.5.1 The fundamental theorem for line integrals
One consequence of this result is that the line integral of a vector field of the form $∇f$ is path independent, i.e. \[ \int_{C_1}\nabla f \pd d\r = \int_{C_2}\nabla f \pd d\r \]
That is, the line integral of a conservative vector field is path independent.
It turns out, the converse is also true. Namely, if $\displaystyle \int_C \F\pd d\r$ is path independet in some region $D$, then $\F$ is conservative. (See Theorem 4 in Stewart 8th ed. pp. 1089-1090)
35.5.1 The fundamental theorem for line integrals
Equivalently,$\displaystyle \int_{C} \F \pd d\r$ is path independent in some
region $D$ if and only if $\displaystyle \oint_{C'}\F\pd d\r = 0$
for every closed path $C'$ in $D$.
Here $\displaystyle "\oint"$ indicates
the line integral over a closed curve.
Let's prove this statement! 🙂
35.5.1 The fundamental theorem for line integrals
Proof: First, recall some properties:
|
|
|
35.5.1 The fundamental theorem for line integrals
|
|
Proof: "$\Rightarrow$" Suppose $\int_C \F\pd d\r $ is path independent in $D$. Then \[ \int_{C_1} \F\pd d\r = \int_{C_2} \F\pd d\r \] for any $C_1$ and $C_2$ in $D$ with the same end points $A$ and $B$. But $\displaystyle \int_{C_2} \F\pd d\r =- \int_{-C_2} \F\pd d\r$. |
35.5.1 The fundamental theorem for line integrals
|
|
Proof: "$\Rightarrow$" $$\displaystyle \int_{C_2} \F\pd d\r =- \int_{-C_2} \F\pd d\r$$ Here $-C_2$ is the same path as $C_2$ but with opposite orientation. Then $\displaystyle 0=$ $\displaystyle \int_{C_1} \F\pd d\r + \int_{-C_2} \F\pd d\r $ $\displaystyle = \int_{C} \F\pd d\r$ where $C$ is any closed path such that $C = C_1 + (-C_2)$ in $D$. $\blacksquare$ |
35.5.1 The fundamental theorem for line integrals
|
|
Proof: "$\Leftarrow$" Suppose $\displaystyle \oint_C \F\pd d\r=0 $ for every closed path $C$ in $D$. Let $A$ and $B$ be points on $C$ ($A\neq B$) and consider $ C_1$ and $C_2$ paths with same end points $A$ and $B$ such that \[ C = C_1 + (-C_2). \] Then $\displaystyle \oint_C \F\pd d\r= \int_{C_1} \F\pd d\r + \int_{-C_2} \F\pd d\r$ So $\displaystyle \int_{C_1} \F\pd d\r + \int_{-C_2} \F\pd d\r=0.$ Or $\displaystyle \int_{C_1} \F\pd d\r - \int_{C_2} \F\pd d\r=0$. Hence $\displaystyle \int_{C_1} \F\pd d\r = \int_{C_2} \F\pd d\r$. $\blacksquare$ |