Calculus &
Linear Algebra II
Chapter 32
32 Spherical coordinates
By the end of this section, you should be able to answer the following questions:
- What is the relationship between rectangular coordinates and spherical coordinates?
- How do you transform a triple integral in rectangular coordinates into one in terms of spherical coordinates?
- What is the Jacobian of the transformation?
32 Spherical coordinates
Sometimes it is useful to use spherical coordinates in order to simplify the integral. This involves the transformation \[ x= r\cos \theta \sin \phi ,\quad y=r\sin \theta \sin \phi , \quad z = r \cos \phi. \qquad (15) \]
In this case $\theta$ is longitude, $\phi$ is co-latitude, and $r$ the distance from the origin.
32 Spherical coordinates
$x= r\cos \theta \sin \phi ,\quad y=r\sin \theta \sin \phi , \quad z = r \cos \phi. \qquad (15)$
32 Spherical coordinates
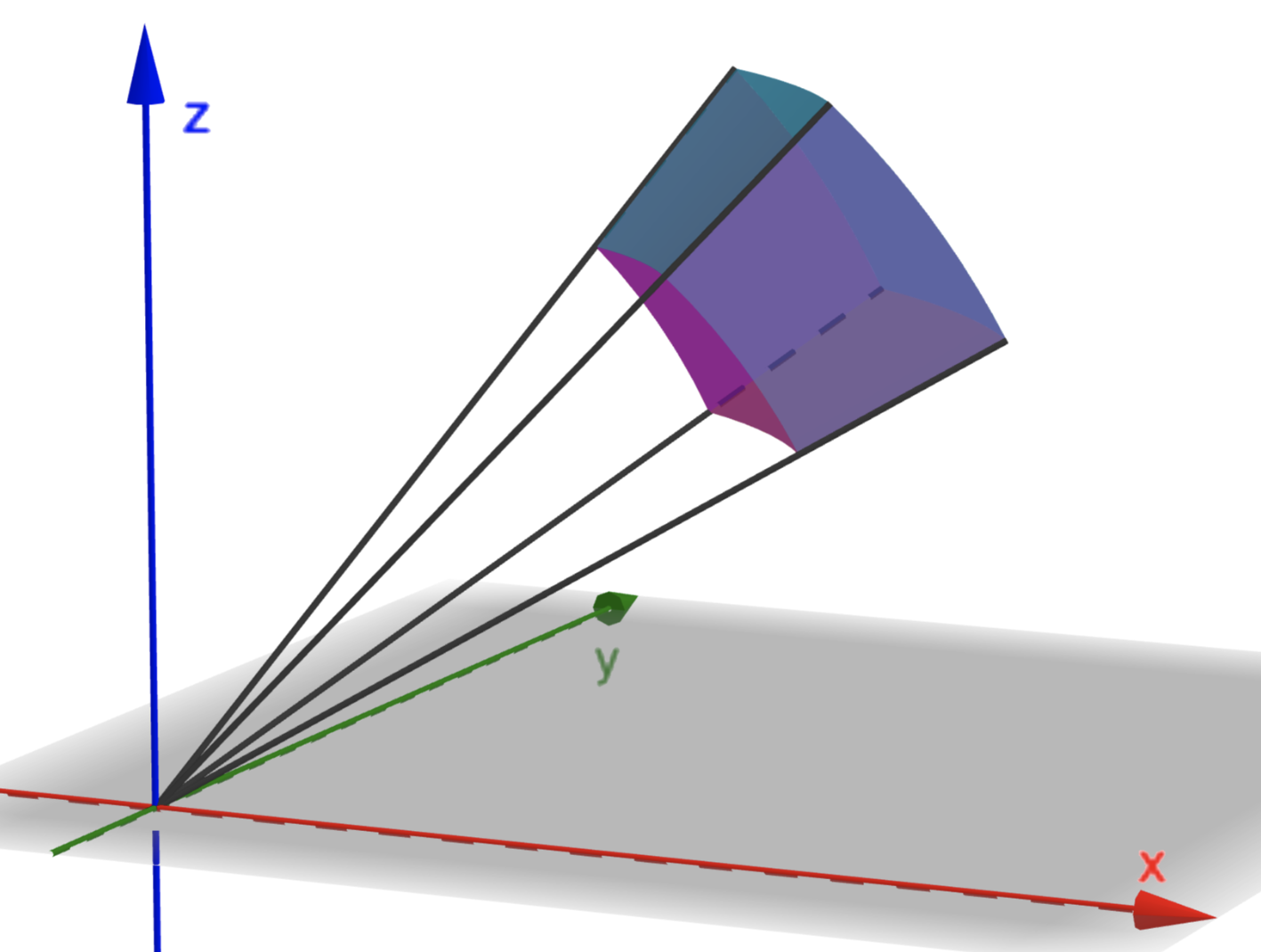
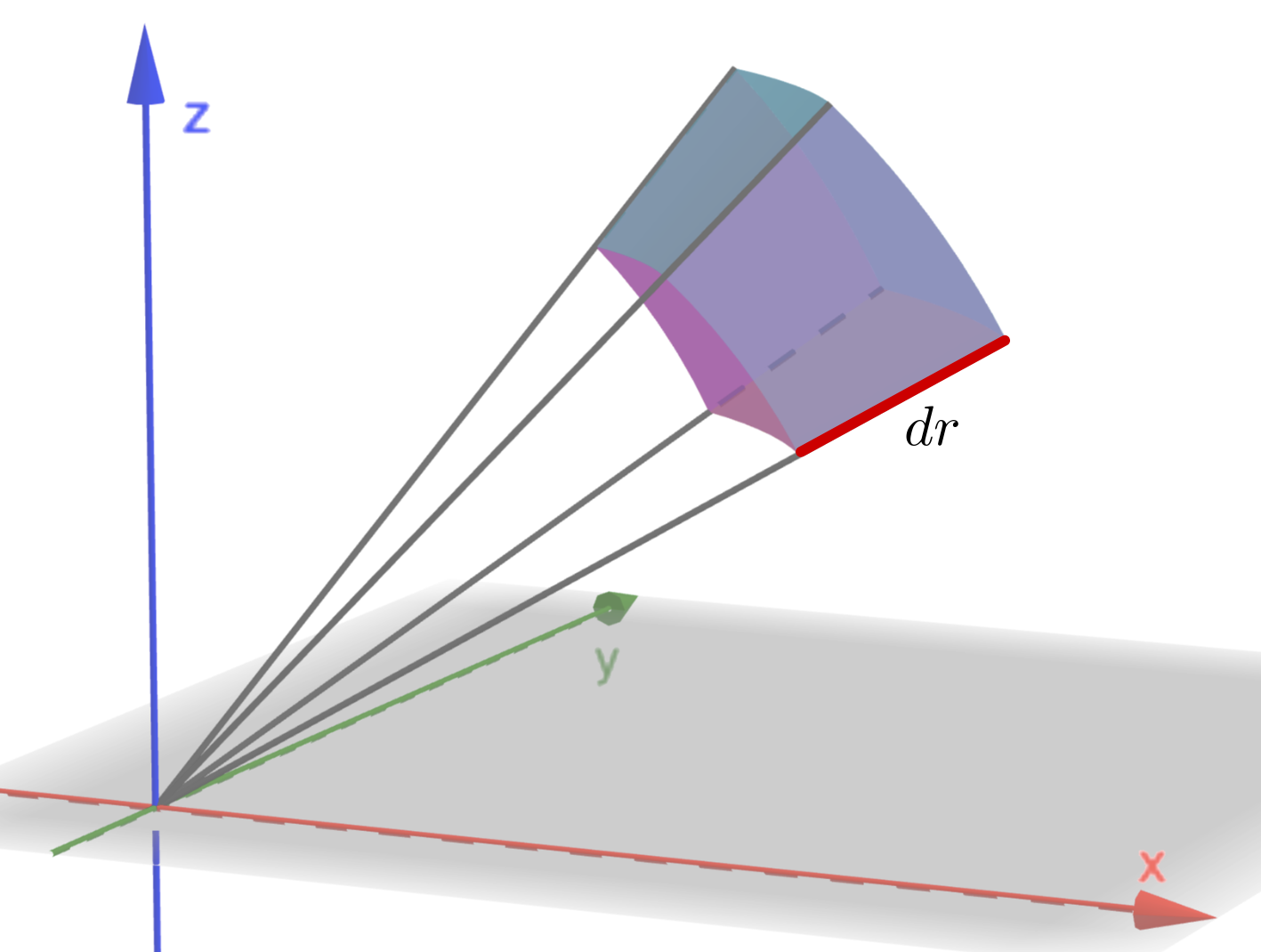
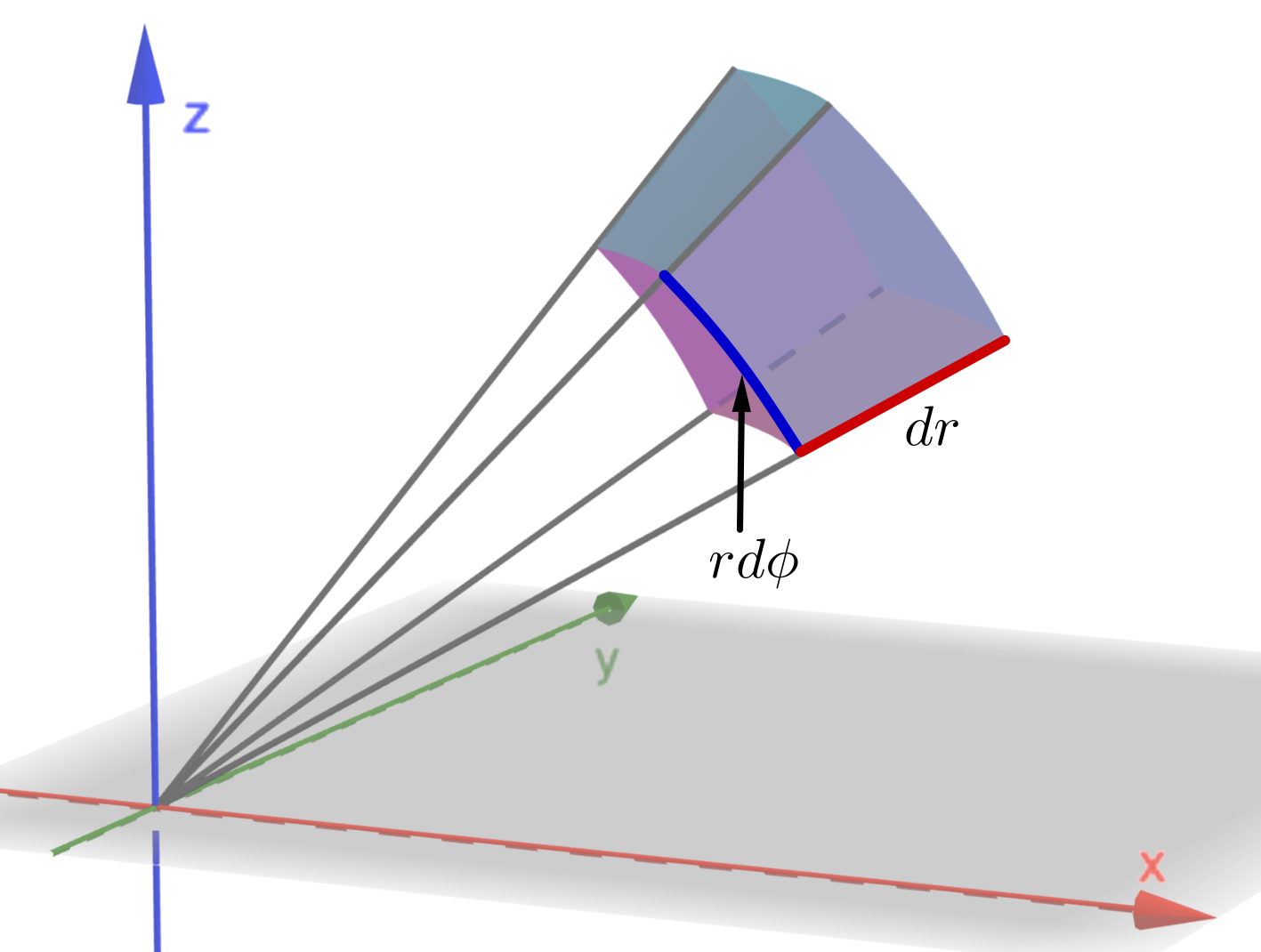
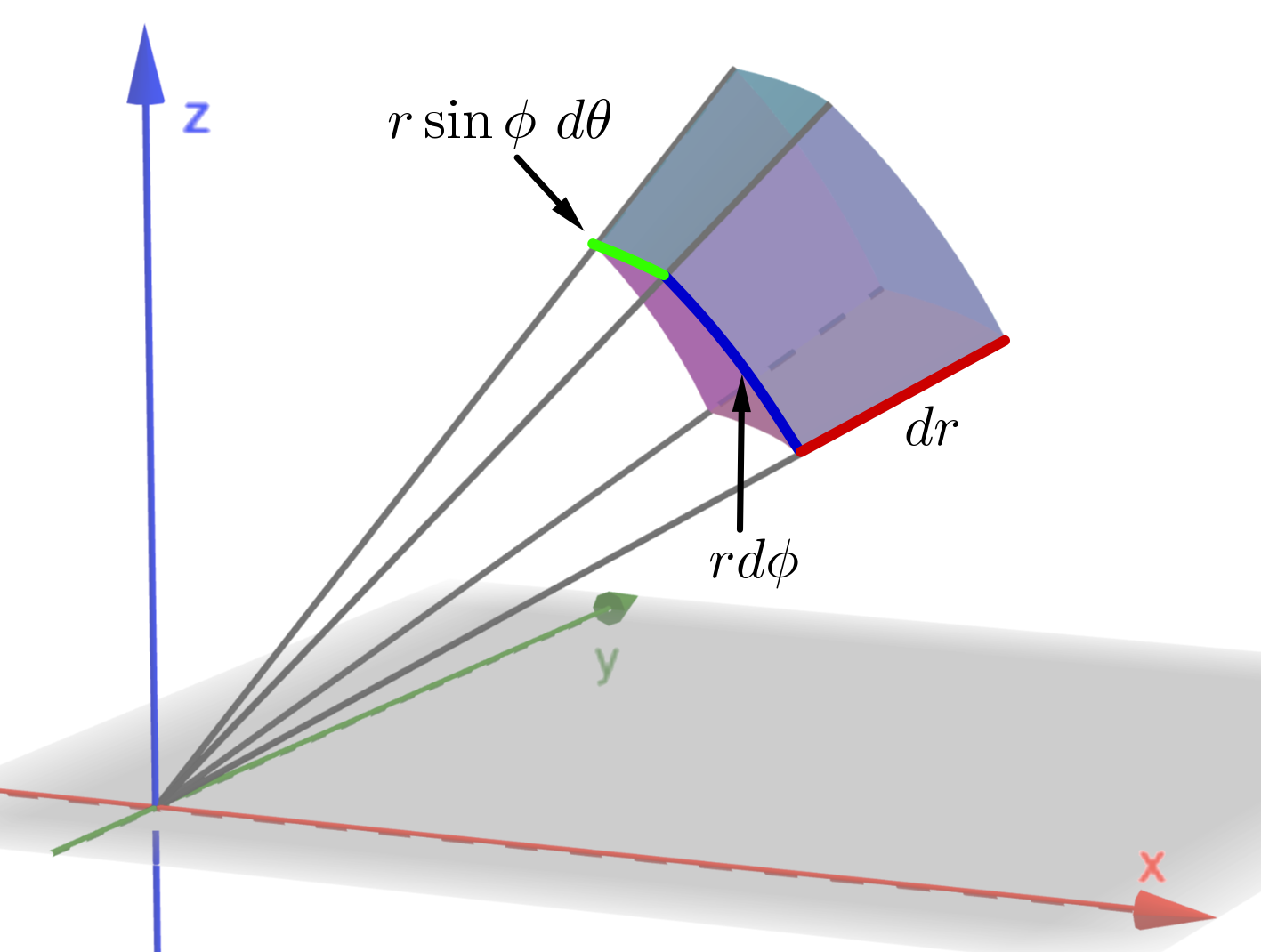
We now aim to calculate a small element of volume of a spherical shell. This will then show how in a triple integral we can transform from rectangular coordinates to spherical coordinates by substituting the transformation (15) and by making the change \[ dx~dy~dz\rightarrow r^2\sin \phi ~dr~d\theta ~d\phi \]
Consider the following diagram.
32 Spherical coordinates
32 Spherical coordinates
32 Spherical coordinates
The important result is that the triple integral in rectangular coordinates transforms as follows:
$\displaystyle \iiint_\limits{R} f(x,y,z) ~dx~dy~dz $
$\displaystyle =\iiint_\limits{S} f\left(r\cos \theta \sin \phi, r \sin \theta \sin \phi, r\cos \phi \right) r^2\sin \phi ~dr~d\theta ~d\phi.$
32.1 A simple example:
Find the volume of a sphere of radius $R$.
32.1 A simple example:
Find the volume of a sphere of radius $R$.
Recall that \[ \text{Volume } = \iiint_V ~dV. \]
We describe the sphere as: \[ 0 \leq r \leq R, \; 0\leq \theta \leq 2 \pi, \; 0\leq \phi \leq \pi. \]
Then \[ V= \{(r,\theta, \phi), ~|~ 0 \leq r \leq R, \; 0\leq \theta \leq 2 \pi, \; 0\leq \phi \leq \pi\}. \]
32.1 A simple example:
Find the volume of a sphere of radius $R.$
| $\text{V } $ | $\displaystyle = \iiint_V dV $ $\displaystyle = \int_{\phi=0}^{\phi=\pi} \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=R} $ $\displaystyle r^2\sin \phi ~dr~d\theta~ d\phi$ |
| $\displaystyle = \left( \int_{\phi=0}^{\phi=\pi} \sin\phi ~d\phi \right) \left( \int_{\theta=0}^{\theta=2\pi}~d\theta \right)\left( \int_{r=0}^{r=R}r^2~dr\right)$ | |
| $\displaystyle = \left( -\cos\phi \Bigg|_{\phi=0}^{\phi=\pi} \right) \left( \theta\Bigg|_{\theta=0}^{\theta=2\pi} \right)\left( \frac{r^3}{3}\Bigg|_{r=0}^{r=R}\right)$ | |
| $\displaystyle = \large 2 ~(2 \pi) \left( \frac{R^3}{3}\right)$ $\displaystyle = \large \frac{4}{3} \pi R^3.$ |
32.2 Find the mass of a sphere of radius $R$
whose density is given by $\rho (x,y,z) = e^{-\left(x^2+y^2+z^2\right)^{1/2}}.$
Recall that $$\displaystyle \iiint_V \rho(x,y,z)~ dV = \iiint_V e^{-\left(x^2+y^2+z^2\right)^{1/2}}~dV.$$
We can't compute this integral in rectangular coordinates! 😥
Let's use spherical coordinates:
$\ds x= r\cos \theta \sin \phi ,\quad y=r\sin \theta \sin \phi , \quad z = r \cos \phi. $
32.2 Find the mass of a sphere of radius $R$
whose density is given by $\rho (x,y,z) = e^{-\left(x^2+y^2+z^2\right)^{1/2}}.$
Then we have that
| $x^2+y^2+z^2 $ | $= r^2 \cos^2\theta \sin^2\phi + r^2 \sin^2\theta \sin^2\phi + r^2 \cos^2 \phi$ |
| $= r^2 \left(\cos^2\theta + \sin^2\theta \right) \sin^2\phi + r^2 \cos^2 \phi$ | |
| $= r^2 \sin^2\phi + r^2 \cos^2 \phi$ $= r^2$. |
Thus $\rho(r,\theta, \phi) = e^{-r}$.
Finally, the region $V$ is described by: \[ 0 \leq r \leq R, \; 0\leq \theta \leq 2 \pi, \; 0\leq \phi \leq \pi. \]
32.2 Find the mass of a sphere of radius $R$
whose density is given by $\rho (x,y,z) = e^{-\left(x^2+y^2+z^2\right)^{1/2}}.$
| $\text{Mass}$ | $\displaystyle =\iiint_V \rho~ dV $ $\displaystyle =\iiint_V e^{-r} ~dV $ |
| $\displaystyle =\int_{\phi=0}^{\phi=\pi} \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=R} e^{-r}$ $r^2\sin\phi ~dr~d\theta~d\phi$ | |
| $\displaystyle = \left(\int_{\phi=0}^{\phi=\pi}\sin \phi~d\phi \right) \left(\int_{\theta=0}^{\theta=2\pi}~d\theta \right)\left(\int_{r=0}^{r=R}r^2e^{-r}~dr\right) $ | |
| $\displaystyle = 2~ (2 \pi ) \int_{r=0}^{r=R}r^2e^{-r}~dr $ $\displaystyle = 4 {\large \pi} \int_{r=0}^{r=R}r^2e^{-r}~dr $ |
32.2 Find the mass of a sphere of radius $R$
The challenge is now to compute: $\displaystyle \int_{r=0}^{r=R}r^2e^{-r}~dr.$
Recall the technique Integration by parts.
Consider the functions $u,$ $v.$ Using the product rule we have
$d(uv) = u ~dv + v ~du $ $\implies u~dv = d(uv) - v~du$ $$\implies \int u~dv = uv - \int v~du$$
32.2 Find the mass of a sphere of radius $R$
Take $u = r^2$ and $dv= e^{-r}~dr.$ So $du = 2r ~dr$ and $v = -e^{-r}.$
| $\displaystyle \int_{r=0}^{r=R}\underbrace{r^2}_{u}\overbrace{e^{-r}~dr}^\text{$dv$} $ | $\displaystyle = \underbrace{r^2}_\text{$u$}\overbrace{\left(-e^{-r}\right)}^\text{$v$}\Bigg|_{r=0}^{r=R} - \int_{r=0}^{r=R}\underbrace{\left(-e^{-r}\right)}_\text{$v$}\overbrace{(2r)~dr}^\text{$du$}$ |
| $\displaystyle = -R^2e^{-R} +2 \int_{r=0}^{r=R}re^{-r}~dr\qquad$ $($A$)$ |
32.2 Find the mass of a sphere of radius $R$
Now take $u = r$ and $dv= e^{-r}~dr.$ So $du = dr$ and $v = -e^{-r}.$
| $\quad\quad($A$)$ | $\displaystyle = -R^2e^{-R} +2 \left[ -re^{-r}\Bigg|_{r=0}^{r=R} - \int_{r=0}^{r=R}\left(-e^{-r}\right)sr \right]$ |
| $\displaystyle = -R^2 e^{-R} - 2R e^{-R} + 2 \int_{r=0}^{r=R}e^{-r}~dr$ | |
| $\displaystyle = -R^2 e^{-R} - 2R e^{-R} + 2 \left[ -e^{-r}\Bigg|_{r=0}^{r=R}\right]$ | |
| $\displaystyle =-R^2 e^{-R} - 2R e^{-R} + 2\left[ -e^{-R}+1 \right]$ | |
| $\displaystyle = 2 - 2e^{-R} - 2Re^{-R} - R^2e^{-R}$ | |
| $\displaystyle = 2 - e^{-R} \left( R^2+2R+2 \right)$. |
32.2 Find the mass of a sphere of radius $R$
whose density is given by $\rho (x,y,z) = e^{-\left(x^2+y^2+z^2\right)^{1/2}}$.
Therefore
| $\text{Mass}$ | $\displaystyle =\iiint_V \rho ~dV $ $\displaystyle =\iiint_V e^{-r}~ dV $ |
| $\displaystyle = 4 {\large \pi } \int_{r=0}^{r=R}r^2e^{-r}~dr $ | |
| $\displaystyle = 4 {\large \pi }\left[2 - e^{-R} \left( R^2+2R+2 \right)\right]. $ |
32.3 Find the volume of the "ice cream cone" $R$
between a sphere of radius $a$ (centred at the origin) and the cone $z=\sqrt{x^2+y^2}$.
32.3 Find the volume of the "ice cream cone" $R$
Let's use spherical coordinates \[ x = r\cos \theta \sin \phi, \quad y = r \sin \theta \sin \phi, \quad z = r \cos \phi. \]
First, the bounds for $r$ and $\theta$ are: \[ 0\leq r \leq a, \qquad 0 \leq \theta \leq 2 \pi. \]
For the bounds for $\phi$ we need consider the cone $z= \sqrt{x^2+y^2}$. Then
| $\displaystyle \quad \quad z $ | $= \sqrt{x^2+y^2}$ $\displaystyle =\sqrt{ r^2\cos^2 \theta \sin^2 \phi + r^2 \sin^2 \theta \sin^2 \phi }$ |
| $r \cos \phi$ |
$\displaystyle =\sqrt{ r^2\sin^2 \phi \left( \cos^2 \theta + \sin^2 \theta\right) }$
|
32.3 Find the volume of the "ice cream cone" $R$
The bounds for $r$ and $\theta$ are: \[ 0\leq r \leq a, \qquad 0 \leq \theta \leq 2 \pi. \]
And
| $r \cos \phi$ | $= r\sin \phi$ |
| $\;\; \tan \phi$ | $= 1,$ with $r\neq 0.$ |
This implies that $\phi = \dfrac{\pi}{4}.$ Then $0\leq \phi \leq \dfrac{\pi}{4},$ Thus \[ E = \left\{ \left(r, \theta, \phi\right) ~|~ 0\leq r \leq a, 0 \leq \theta \leq 2 \pi, 0\leq \phi \leq \dfrac{\pi}{4}\right\}. \]
32.3 Find the volume of the "ice cream cone" $R$
| $\text{V}$ | $\displaystyle = \iiint_E~ dV$ |
| $\displaystyle = \int_{\phi=0}^{\phi =\pi/4} \int_{\theta=0}^{\theta =2\pi} \int_{r=0}^{r = a} r^2\sin\phi ~dr ~d\theta ~d\phi$ | |
| $\displaystyle = \left( \int_{\phi=0}^{\phi= \pi/4} \sin\phi ~d\phi \right) \left( \int_{\theta=0}^{\theta= 2\pi} ~d\theta \right) \left( \int_{r=0}^{r = a}r^2~dr \right) $ | |
| $\displaystyle = \left( 1 - \frac{\sqrt{2}}{2} \right) \left(2 {\large \pi} \right) \left( \frac{a^3}{3} \right) $ $\displaystyle = \left( 1 - \frac{\sqrt{2}}{2} \right) \frac{2 {\large \pi} a^3}{3} . $ |