Calculus &
Linear Algebra II
Chapter 31
31 Cylindrical coordinates
By the end of this section, you should be able to answer the following questions:
- What is the relationship between rectangular coordinates and cylindrical coordinates?
- How do you transform a triple integral in rectangular coordinates into one in terms of cylindrical coordinates?
- What is the Jacobian of the transformation?
31 Cylindrical coordinates
Sometimes it is useful to use cylindrical coordinates in order to simplify the integral. This involves the transformation
$ x= r\cos \theta ,\quad y=r\sin \theta, \quad z =z. \qquad (14) $
31 Cylindrical coordinates
$x= r\cos \theta ,\quad y=r\sin \theta, \quad z =z. \qquad (14)$
31 Cylindrical coordinates
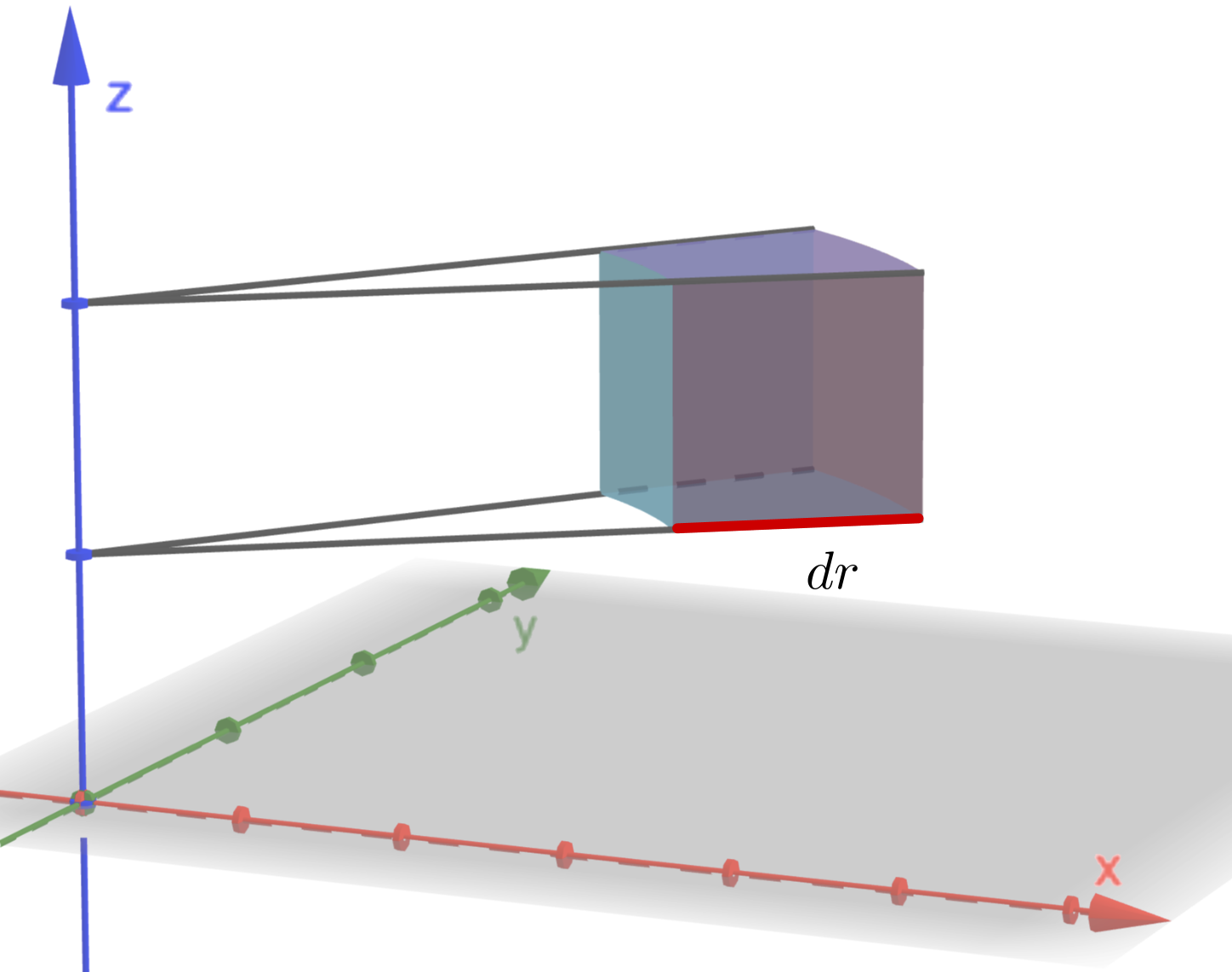
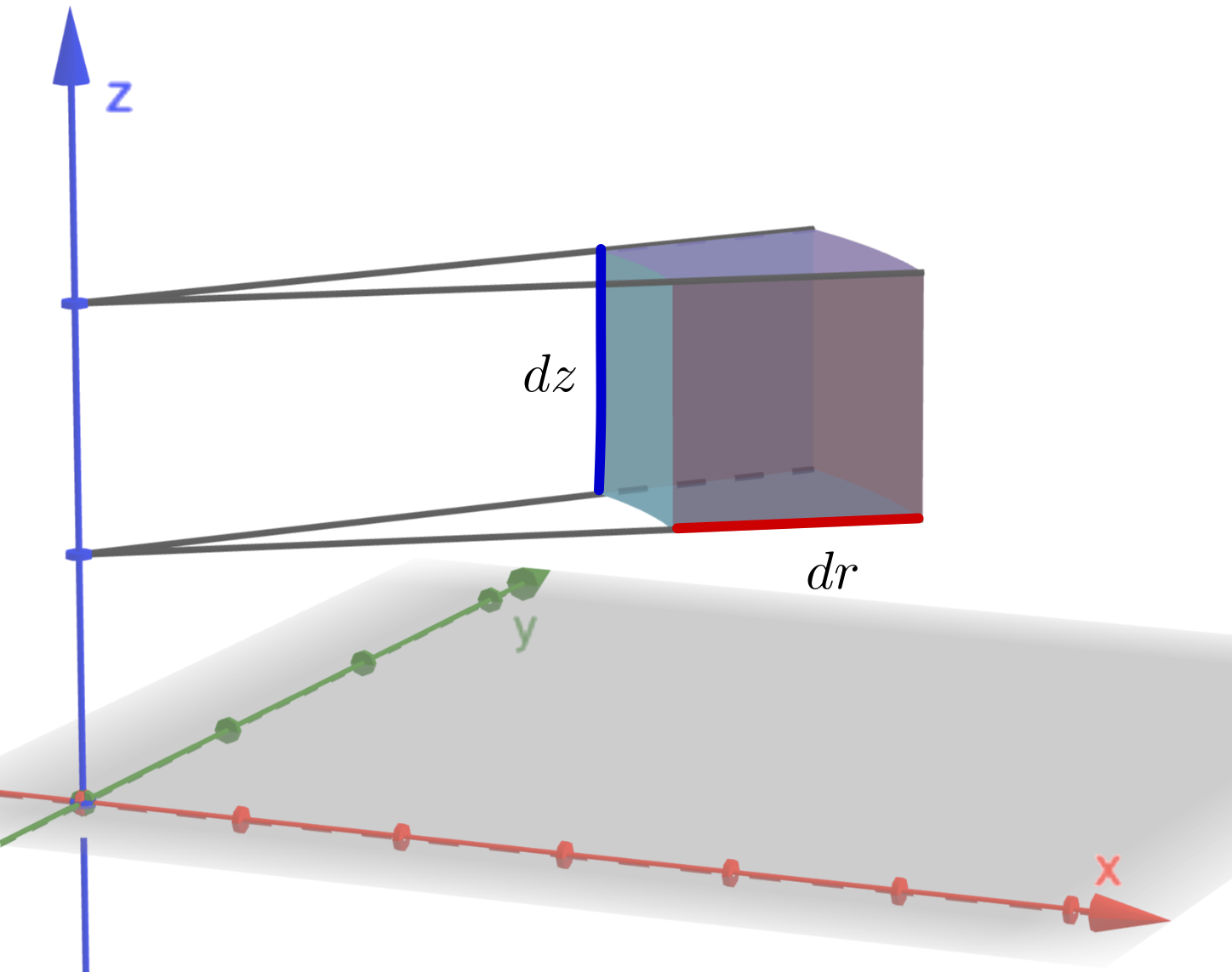
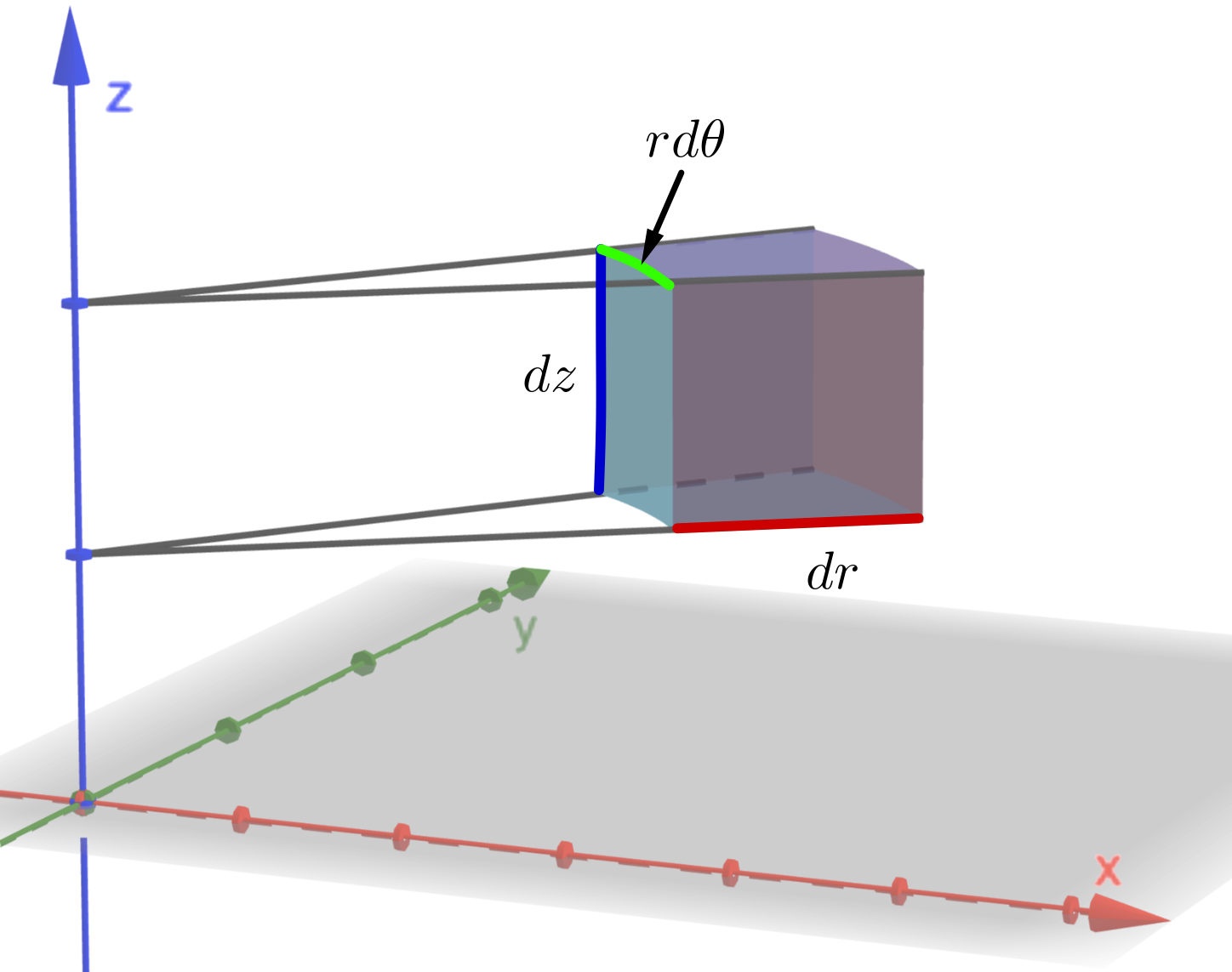
We now aim to calculate a small element of volume of a cylindrical shell. This will then show how in a triple integral we can transform from rectangular coordinates to cylindrical coordinates by substituting the transformation (14) and by making the change \[ dx~dy~dz\rightarrow r~dr~d\theta ~dz \]
31 Cylindrical coordinates
Consider the following diagram.
32 Spherical coordinates

31 Cylindrical coordinates
The important result is that the triple integral in rectangular coordinates transforms as follows: \[ \iiint_\limits{R} f(x,y,z) ~dx~dy~dz = \iiint_\limits{C} f\left(r\cos \theta , r \sin \theta, z \right) r~dr~d\theta ~dz. \]
31.1 A simple example: Find the volume of a cylinder of radius $R$ and height $H.$ (Ans. $\pi~ R^2 H$)
Recall that if $f(x,y)\geq 0,$ then the double integral can be interpreted as the volume under the surface $z=f(x,y).$
If $f(x,y,z)\geq 0,$ then the triple integral can be interpreted as the "hypervolume" of a $4D$ object.
This is very difficult to visualise. 😕
31.1 A simple example: Find the volume of a cylinder of radius $R$ and height $H.$ (Ans. $\pi~ R^2 H$)
Consider the special case where $f(x,y,z)=1$ for every $(x,y,z)\in E,$ the domain of $f.$ Then the triple integral represents the volume of $E.$ That is \[ \iiint_E 1 ~dV = \text{Volume of } E. \]
Here we are going to use cylindrical coordinates \[ x= r\cos \theta ,\quad y=r\sin \theta, \quad z =z. \]
So we have that \[ 0\leq r \leq R,\quad 0\leq \theta \leq 2\pi,\quad 0\leq z \leq H. \]
31.1 A simple example: Find the volume of a cylinder of radius $R$ and height $H.$ (Ans. $\pi~ R^2 H$)
Then
| $\text{V} $ | $\displaystyle = \iiint_E ~dV$ $\displaystyle = \int_{z=0}^{z=H} \int_{r=0}^{r=R} \int_{\theta=0}^{\theta=2\pi} r~d\theta~ dr ~dz$ |
| $\displaystyle = \left( \int_{\theta=0}^{\theta=2\pi} ~d\theta \right) \left( \int_{r=0}^{r=R} r~dr\right) \left(\int_{z=0}^{z=H} dz\right)$ | |
| $\displaystyle = \large 2\pi ~\frac{R^2}{2} H $ $\displaystyle = \large \pi ~R^2 H.$ |
31.2 Find the mass of the solid defined by
the region contained within the cylinder $x^2 + y^2 = 1$ below the plane $z = 4$ and above the paraboloid $z = 1- x^2 y^2.$ The density at any given point in the region is proportional to the distance from the axis of the cylinder.
31.2 Find the mass of the solid defined by
the region contained within the cylinder $x^2 + y^2 = 1$ below the plane $z = 4$ and above the paraboloid $z = 1- x^2 y^2$. The density at any given point in the region is proportional to the distance from the axis of the cylinder.
It is given that $\rho \propto$ distance from $z$-axis. That is \[ \rho \propto \sqrt{\left(x-0\right)^2+\left(y-0\right)^2+\left(z-z\right)^2} = \sqrt{x^2+y^2} \] If we take $\rho = k \sqrt{x^2+y^2},$ with $k$ the constant of proportionality, then \[\text{Mass} = \iiint_V\rho ~dV = \iiint_V k \sqrt{x^2+y^2}dV\]
31.2 Find the mass of the solid (cont.)
It is easier to compute this integral using cylindrical coordinates \[ x= r\cos \theta ,\quad y=r\sin \theta, \quad z =z. \]
So we have that
$z = 1-x^2-y^2 $ $= 1 - r^2\cos ^2 \theta- r^2 \sin^2 \theta $ $= 1 - r^2$.
Thus $1-r^2\leq z \leq 4.$ On the other hand, the domain $D$ for $x,y$ is constrained by $x^2+y^2=1.$ So \[ 0\leq r\leq 1,\quad 0\leq \theta \leq 2 \pi. \]
\[ \Ra \,V = \left\{(r, \theta, z) ~|~ 1-r^2\leq z \leq 4, 0\leq r\leq 1, 0\leq \theta \leq 2 \pi \right\} \]
31.2 Find the mass of the solid (cont.)
| $\text{Mass} $ | $\displaystyle = \iiint_V\rho ~dV= \iiint_V k \sqrt{x^2+y^2}dV$ |
| $\displaystyle = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \int_{z=1-r^2}^{z=4} k~ r~ r ~dz~dr~d\theta$ | |
| $\displaystyle = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \left[ k~ r^2 ~z \Bigg|_{z=1-r^2}^{z=4}\right] dr~d\theta$ | |
| $\displaystyle = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} k r^2 \left(4 - \left(1-r^2\right)\right) dr~d\theta$ | |
| $\displaystyle = \left( \int_{\theta=0}^{\theta=2\pi} d\theta \right) \left( \int_{r=0}^{r=1} k r^2 \left(3 + r^2\right) dr\right)$ $=\ds \large \frac{12 \pi k}{5}.$ |