Calculus &
Linear Algebra II
Chapter 13
13 Least squares function approximation
Problem: Given a function f∈C[a,b], find the best approximation to f using only functions from a specified subspace U of C[a,b].
Interpret "best possible" in the sense of least squares.
Consider g as an approximation to f as shown by the graph.
13 Least squares function approximation
At point x0 the error is |f(x0)−g(x0)|. For the entire interval, define error as ∫ba|f(x)−g(x)|dx. This is area between curves.
13 Least squares function approximation
An easier definition (and one more amenable to calculations) is the mean squared error (MSE) MSE=∫ba(f(x)−g(x))2 dx. Use the integral inner product on C[a,b] defined by ⟨p,q⟩=∫bap(x)q(x) dx
⇒ MSE =||f−g||2=⟨f−g,f−g⟩=∫ba(f(x)−g(x))2 dx.
13 Least squares function approximation
⟹ MSE =||f−g||2=⟨f−g,f−g⟩=∫ba(f(x)−g(x))2 dx.
It follows that the best approximation to f using only functions g's from the subspace U of C[a,b] is achieved by minimizing ||f−g||2 relative to the above integral inner product.
13.1 Example: sin(x)
Find the least squares approximation for sinx in the subspace of C[0,π] spanned by {1,x,x2}. Use the inner product ⟨p,q⟩=∫π0p(x)q(x) dx.
Look for p(x)∈U such that ‖ is minimal.
13.1 Example: \sin(x)
Find the least squares approximation for \sin x in the subspace of C[0,\pi] spanned by \{1,x,x^2\}. Use the inner product \langle \mathbf{p},\mathbf{q}\rangle =\int_0^\pi p(x)q(x)~dx.
Look for p(x)\in U such that \norm{\sin x - p(x)}^2 = \int_0^{\pi} \big(\sin x- p(x) \big)dx is minimal. From Chapter 12, the best approximation p(x) for \sin x is given by p(x) = \mathrm{Proj}_{U}(\sin x).
From Chapter 12, the best approximation p(x) for \sin x is given by
\ds p(x) = \mathrm{Proj}_{U}(\sin x).
13.1 Example: \sin(x)
Find the least squares approximation for \sin x in the subspace of C[0,\pi] spanned by \{1,x,x^2\}. Use the inner product \langle \mathbf{p},\mathbf{q}\rangle =\int_0^\pi p(x)q(x)~dx.
We actually have two methods from Chapter 12.
Solution 1. Use the Gram-Schmidt process to turn \beta into an orthonormal basis \{\hat{\bfe}_1, \hat{\bfe}_2, \hat{\bfe}_3\}. Then p(x) = \mathrm{Proj}_{U}(\sin x) is given by p(x) = \mathrm{Proj}_{U}(\sin x) \qquad \qquad \qquad \qquad \qquad \qquad \qquad \; = \big\langle\sin x , \hat{\bfe}_1\big\rangle\hat{\bfe}_1 + \big\langle\sin x , \hat{\bfe}_2\big\rangle\hat{\bfe}_2 + \big\langle\sin x , \hat{\bfe}_3\big\rangle\hat{\bfe}_3. This gives the best approximation for \sin x by functions from U.
13.1 Example: \sin(x)
Find the least squares approximation for \sin x in the subspace of C[0,\pi] spanned by \{1,x,x^2\}. Use the inner product \langle \mathbf{p},\mathbf{q}\rangle =\int_0^\pi p(x)q(x)~dx.
We actually have two methods from Chapter 12.
Solution 1. Use the Gram-Schimdt process to turn \beta into an orthonormal basis \{\hat{\bfe}_1, \hat{\bfe}_2, \hat{\bfe}_3\}. Then p(x) = \mathrm{Proj}_{U}(\sin x) is given by p(x) = \mathrm{Proj}_{U}(\sin x) = \big\langle\sin x , \hat{\bfe}_1\big\rangle\hat{\bfe}_1 + \big\langle\sin x , \hat{\bfe}_2\big\rangle\hat{\bfe}_2 + \big\langle\sin x , \hat{\bfe}_3\big\rangle\hat{\bfe}_3. This gives the best approximation for \sin x by functions from U.
Exercise: 📝 1) Find the orthonormal basis; 2) Compute \big\langle \sin x, \hat{\bfe}_i \big\rangle for i=1,2,3; and, 3) Verify the answer is given by p(x) = \frac{12\left(\pi^2-10\right)}{\pi^3} +\frac{60\left(12-\pi^2\right)}{\pi^4}x +\frac{60\left(\pi^2-12\right)}{\pi^5}x^2.
13.1 Example: \sin(x)
Find the least squares approximation for \sin x in the subspace of C[0,\pi] spanned by \{1,x,x^2\}; with \langle \mathbf{p},\mathbf{q}\rangle =\int_0^\pi p(x)q(x)~dx.
Solution 2. Set p(x) = \alpha_1 + \alpha_2 x + \alpha_3 x^2. Then \alpha_1, \alpha_2,\alpha_3 are determined by \left( \begin{array}{ccc} \langle 1, 1 \rangle & \langle 1, x \rangle & \langle 1, x^2 \rangle \\ \langle x, 1 \rangle & \langle x, x \rangle & \langle x, x^2 \rangle \\ \langle x^2, 1 \rangle & \langle x^2, x \rangle & \langle x^2, x^2 \rangle \\ \end{array} \right) \left( \begin{array}{c} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \end{array} \right) = \left( \begin{array}{c} \langle \sin x, 1 \rangle \\ \langle \sin x, x \rangle \\ \langle \sin x, x^2 \rangle \\ \end{array} \right) \ds \int_0^{\pi}x^ndx = \frac{\pi^{n+1}}{n+1},\, \,\langle \sin x, 1 \rangle = 2, \,\langle \sin x, x \rangle = \pi, \,\langle \sin x, x^2 \rangle = \pi^2-4.
\ds\Ra \left( \begin{array}{ccc} \pi & \frac{\pi^2}{2} & \frac{\pi^3}{3} \\ \frac{\pi^2}{2} & \frac{\pi^3}{3} & \frac{\pi^4}{4} \\ \frac{\pi^3}{3} & \frac{\pi^4}{4} & \frac{\pi^5}{5} \\ \end{array} \right) \left( \begin{array}{c} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \end{array} \right) = \left( \begin{array}{c} 2\\ \pi \\ \pi^2-4 \\ \end{array} \right)
13.1 Example: \sin(x)
Find the least squares approximation for \sin x in the subspace of C[0,\pi] spanned by \{1,x,x^2\}; with \langle \mathbf{p},\mathbf{q}\rangle =\int_0^\pi p(x)q(x)~dx.
Solution 2. Set p(x) = \alpha_1 + \alpha x + \alpha_3 x^2. Then \alpha_1, \alpha_2,\alpha_3 are determined by
\left( \begin{array}{ccc} \pi & \dfrac{\pi^2}{2} & \dfrac{\pi^3}{3} \\ \dfrac{\pi^2}{2} & \dfrac{\pi^3}{3} & \dfrac{\pi^4}{4} \\ \dfrac{\pi^3}{3} & \dfrac{\pi^4}{4} & \dfrac{\pi^5}{5} \\ \end{array} \right) \left( \begin{array}{c} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \end{array} \right) = \left( \begin{array}{c} 2\\ \pi \\ \pi^2-4 \\ \end{array} \right)
Solving this system we get same result from Solution 1. 😃 That is: \alpha_1 = \frac{12\left(\pi^2-10\right)}{\pi^3},\;\; \alpha_2 = \frac{60\left(12-\pi^2\right)}{\pi^4},\;\; \alpha_3 = \frac{60\left(\pi^2-12\right)}{\pi^5}.
13.1 Example: \sin(x)
Find the least squares approximation for \sin x in the subspace of C[0,\pi] spanned by \{1,x,x^2\}; with \langle \mathbf{p},\mathbf{q}\rangle =\int_0^\pi p(x)q(x)~dx.
13.2 Fourier coefficients
In C[0,2\pi], the set \beta_n=\big\{\tfrac{1}{\sqrt{2\pi}}\big\}\cup\big\{\tfrac{1}{\sqrt{\pi}}\cos kx\,|\,k=1,\ldots,n\big\} \cup\big\{\tfrac{1}{\sqrt{\pi}}\sin kx\,|\,k=1,\ldots,n\big\}, where n\in\mathbb{N}_0, is orthonormal with respect to the inner product \langle{\bf f},{\bf g}\rangle=\int_0^{2\pi}f(x)g(x)dx.
13.2 Fourier coefficients
In C[0,2\pi], the set \beta_n=\big\{\tfrac{1}{\sqrt{2\pi}}\big\}\cup\big\{\tfrac{1}{\sqrt{\pi}}\cos kx\,|\,k=1,\ldots,n\big\} \cup\big\{\tfrac{1}{\sqrt{\pi}}\sin kx\,|\,k=1,\ldots,n\big\}, where n\in\mathbb{N}_0, is orthonormal with respect to the inner product \langle{\bf f},{\bf g}\rangle=\int_0^{2\pi}f(x)g(x)dx.
Proof: First note that \Big\langle \dfrac{1}{\sqrt{2\pi} }, \dfrac{1}{\sqrt{2\pi} } \Big\rangle = 1; \Big\langle \dfrac{1}{\sqrt{2\pi} }, \cos(kx) \Big\rangle = 0; \Big\langle \dfrac{1}{\sqrt{2\pi} }, \sin (kx) \Big\rangle = 0. Then \dfrac{1}{\sqrt{2\pi}} is a unit vector perpendicular to each element in \left\{\dfrac{1}{\sqrt{2\pi}} \cos (kx), \dfrac{1}{\sqrt{2\pi}}\sin (kx)~|~ k=1,\ldots, n\right\}.
13.2 Fourier coefficients
Proof: Then
\big\langle \cos \left(kx\right), \cos\left(k'x\right) \big\rangle
| = \ds\int_{0}^{2\pi} \cos \left(kx\right) \cos \left(k'x\right)dx | |
| =\ds \int_{0}^{2\pi} \frac{1}{2} \big[\cos \left( \left( k -k' \right)x \right) +\cos \left( \left( k +k' \right)x \right) \big]dx | |
| =\ds \left\{ \begin{array}{ll} \dfrac{1}{2} \left[ \dfrac{\sin \left( \left( k -k' \right)x \right)}{k-k'} + \dfrac{\sin \left( \left( k +k' \right)x \right)}{k+k'} \right]\Bigg|_0^{2\pi}, & k\neq k' \\ \dfrac{1}{2} \left[ x + \dfrac{\sin \left( 2k x \right)}{2k} \right]\Bigg|_0^{2\pi}, & k= k' \\ \end{array} \right. |
13.2 Fourier coefficients
Proof: Then
\big\langle \cos \left(kx\right), \cos\left(k'x\right) \big\rangle
\qquad= \ds
\left\{
\begin{array}{ll}
\dfrac{1}{2} \left[ \dfrac{\sin \left( \left( k -k' \right)x \right)}{k-k'} + \dfrac{\sin \left( \left( k +k' \right)x \right)}{k+k'} \right]\Bigg|_0^{2\pi}, & k\neq k' \\
\dfrac{1}{2} \left[ x + \dfrac{\sin \left( 2k x \right)}{2k} \right]\Bigg|_0^{2\pi}, & k= k' \\
\end{array}
\right.
=\ds
\left\{
\begin{array}{cc}
0, & k\neq k' \\
{\large \pi}, & k= k' \\
\end{array}
\right. . \qquad\qquad\qquad\qquad\qquad \;\;\qquad
Thus \ds\left\{\frac{1}{\sqrt{ \pi }}\cos (kx )~|~ k=1, \ldots, n\right\} is orthonormal.
13.2 Fourier coefficients
Proof: Similarly we can compute other inner products to obtain
| \big\langle \sin \left(kx\right), \sin\left(k'x\right) \big\rangle | = | \ds \int_0^{2\pi} \sin \left(kx\right) \sin \left(k'x\right)dx |
| = | \ds \left\{ \begin{array}{cc} 0, & k\neq k' \\ \pi, & k= k' \\ \end{array} \right. |
So \ds\left\{\frac{1}{\sqrt{ \pi }}\sin (kx )~|~ k=1, \ldots, n\right\} is orthonormal.
13.2 Fourier coefficients
Proof: Finally
| \big\langle \sin \left(kx\right), \cos\left(k'x\right) \big\rangle | = | \ds \int_0^{2\pi} \sin \left(kx\right) \cos \left(k'x\right)dx |
| = | 0,\; for any k,k'. |
Thus \ds\left\{\frac{1}{\sqrt{ \pi }}\sin (kx )~|~ k=1, \ldots, n\right\} is perpendicular to \ds\left\{\frac{1}{\sqrt{ \pi }}\cos (kx )~|~ k=1, \ldots, n\right\} .
13.2 Fourier coefficients
It follows that \beta_n is an orthonormal basis for the (2n+1)-dimensional subspace W_n=\mathrm{span}(\beta_n) of C[0,2\pi]. The orthogonal projection of {\bf f}\in C[0,2\pi] onto W_n is given by \mathrm{Proj}_{W_n}({\bf f}). In the limit n\to\infty, the corresponding approximation of f(x) yields the Fourier series of f(x) over the interval [0,2\pi]: f(x)=\frac{a_0}{2}+\sum_{k=1}^\infty\,(a_k\cos kx+b_k\sin kx), \text{where } \;a_k=\frac{1}{\pi}\int_0^{2\pi}f(x)\cos kx\,dx,\;\; b_k=\frac{1}{\pi}\int_0^{2\pi}f(x)\sin kx\,dx, are the associated Fourier coefficients.
13.2 Fourier coefficients
To see this we need to find \big \langle \mathbf f, \hat{\bfe}_k \big \rangle\hat{\bfe}_k in the sum.
For \hat{\bfe}_0 = \dfrac{1}{\sqrt{2\pi}}:
\big\langle \mathbf f, \hat{\bfe}_0 \big\rangle\hat{\bfe}_0
= \ds\left(\int_0^{2\pi} f(x) \frac{1}{\sqrt{2\pi}}dx \right) \frac{1}{\sqrt{2\pi}}
= \ds\frac{a_0}{2},\;
where \ds a_0 = \frac{1}{\pi} \int_0^{2\pi} f(x) dx.
13.2 Fourier coefficients
For \hat{\bfe}_k = \dfrac{1}{\sqrt{\pi}}\cos (kx):
\big\langle \mathbf f, \hat{\bfe}_k \big\rangle\hat{\bfe}_k
= \ds\left(\int_0^{2\pi} f(x) \frac{1}{\sqrt{\pi}} \cos(kx) dx \right) \frac{1}{\sqrt{\pi}}\cos (kx)
= \ds a_k\cos (kx),\;
where \ds a_k = \frac{1}{\pi} \int_0^{2\pi} f(x)\cos(kx) dx.
13.2 Fourier coefficients
For \hat{\bfe}_k = \dfrac{1}{\sqrt{\pi}}\sin (kx):
\big\langle \mathbf f, \hat{\bfe}_k \big\rangle\hat{\bfe}_k
= \ds\left(\int_0^{2\pi} f(x) \frac{1}{\sqrt{\pi}} \sin(kx) dx \right) \frac{1}{\sqrt{\pi}} \sin (kx)
= \ds b_k\sin (kx),\;
where \ds b_k = \frac{1}{\pi} \int_0^{2\pi} f(x)\sin(kx) dx.
13.2 Fourier coefficients
For \hat{\bfe}_0 = \dfrac{1}{\sqrt{2\pi}}:
\big\langle \mathbf f, \hat{\bfe}_0 \big\rangle\hat{\bfe}_0 = \ds\frac{a_0}{2},\; where \ds a_0 = \frac{1}{\pi} \int_0^{2\pi} f(x) dx.
For \hat{\bfe}_k = \dfrac{1}{\sqrt{\pi}}\cos (kx):
\big\langle \mathbf f, \hat{\bfe}_k \big\rangle\hat{\bfe}_k = \ds a_k\cos (kx),\; where \ds a_k = \frac{1}{\pi} \int_0^{2\pi} f(x)\cos(kx) dx.
For \hat{\bfe}_k = \dfrac{1}{\sqrt{\pi}}\sin (kx):
\big\langle \mathbf f, \hat{\bfe}_k \big\rangle\hat{\bfe}_k = \ds b_k\sin (kx),\; where \ds b_k = \frac{1}{\pi} \int_0^{2\pi} f(x)\sin(kx) dx.
More about Fourier series (Not examinable)
The Fourier series of a real function f defined on the interval (-p,p) is given by f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left(a_n\,\cos \left(\frac{n\, \pi}{p}x\right)+b_n\,\sin \left(\frac{n\, \pi}{p}x\right) \right), where \begin{eqnarray*} a_0&=&\frac{1}{p}\int_{-p}^pf(x)\,dx,\\ a_n&=&\frac{1}{p}\int_{-p}^pf(x)\,\cos \left(\frac{n\, \pi}{p}x\right)\,dx,\\ b_n&=&\frac{1}{p}\int_{-p}^pf(x)\,\sin \left(\frac{n\, \pi}{p}x\right)\,dx. \end{eqnarray*}
The Fourier series is named in honor of Jean Baptiste Joseph Fourier (1768-1830).
More about Fourier series (Not examinable)
Example: Consider the function defined by f(x)=x+\pi for -\pi < x < \pi and f(x)=f(x+2\pi) for -\infty < x < \infty. Its Fourier series expansion is f(x)=\pi+2\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n+1}}{n}\sin (n\,x).
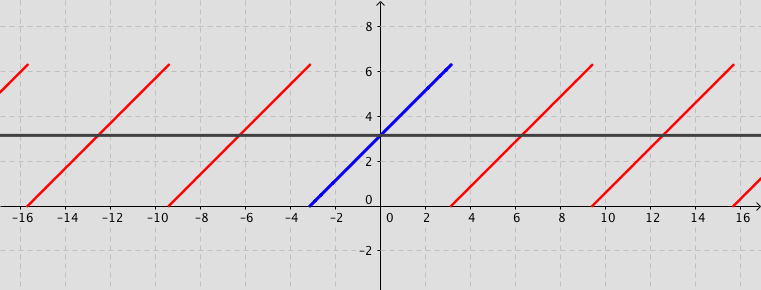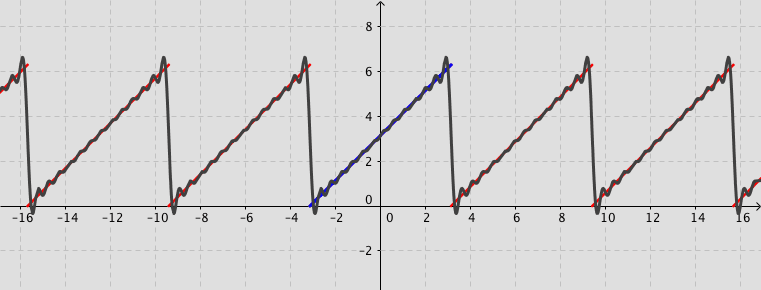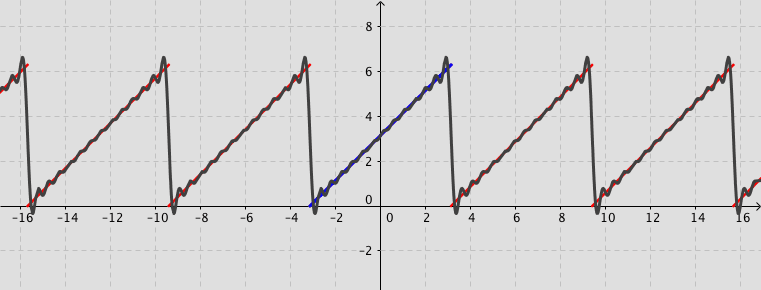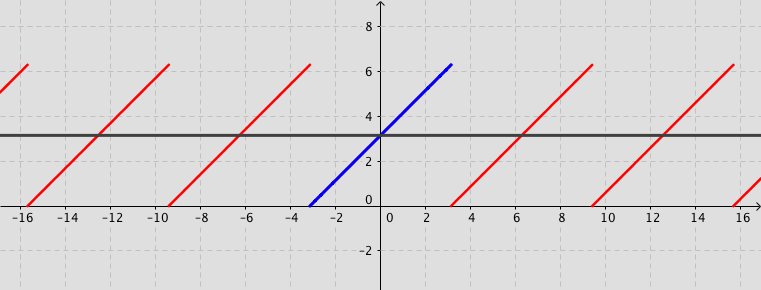
More about Fourier series (Not examinable)
The square wave
More about Fourier series (Not examinable)
|
The square wave Applets inspired by: Jez Swanson |
|
Fourier series: General example
The Cat curve 🐈
Source: Trigonometric interpolation
Credits
Lecture notes based upon the
MATH2001/7000 Workbook
Design, Images & Applets
Juan Carlos Ponce Campuzano
unless otherwise stated
❤️ Support this project ❤️
Patreon