Final remarks
ODEs
Final remarks
First and second order ODEs are amazing! 😃
You learnt about its applications and how we can use them
to model different phenomena! 😎
Final remarks
Now you have super powers (analytic methods)
to solve them! 🚀
- $\ds \dfrac{dC}{dt} = r - \alpha C, \; \alpha>0.$
- $y''+ 6y'+ 9 y =0, \; y(0)=2,\,y'(0)=0.$
- $y'' + 4 y'+5y = 12 \cos x + 4 \sin x.$
- $\ds \dfrac{dP}{dt} = r P\left(1-\frac{P}{\theta}\right),\,r>0,\,\theta>0.$
😱 😵💫 😬 😭
🤔 🤩 🙂 😎
Final remarks
Eventough sometimes they are quite hard to solve them,
we still can model different phenomena with them! 😎
|
$$x^2\dfrac{d^2y}{dx^2} + x\dfrac{dy}{dx} + \left(x^2-\alpha^2 \right) y = 0 ,$$ $$\alpha \in \C.$$ |
We can make fun simulations! 😃
Or, more serious, simulations: The solar system 🤯!
🦋 Lorenz Attractor! 🦋
$\left\{ \begin{eqnarray*} \frac{dx}{dt}&=&\sigma (-x + y)\\ \frac{dy}{dt}&=& -x z + \rho x - y \\ \frac{dz}{dt}&=& x y - \beta z \end{eqnarray*}\right.$
Final remarks
It gets even more interesting when we consider
Partial Differential Equations
For example, Laplace equation
$\dfrac{\partial^2u }{\partial x^2} + \dfrac{\partial^2u}{\partial y^2}+ \dfrac{\partial^2u }{\partial z^2}=0$
Final remarks
It gets even more interesting when we consider
Partial Differential Equations
Wave equation
$\dfrac{\partial^2u }{\partial t^2} = c^2\left( \dfrac{\partial^2u }{\partial x_1^2} + \dfrac{\partial^2u }{\partial x_2^2} + \cdots + \dfrac{\partial^2u }{\partial x_n^2} \right)$

Author: BrentHFoster
Final remarks
It gets even more interesting when we consider
Partial Differential Equations
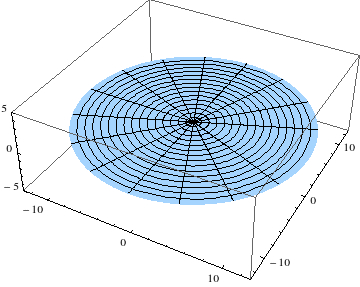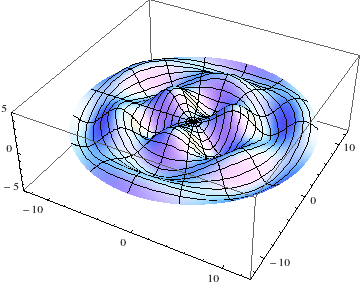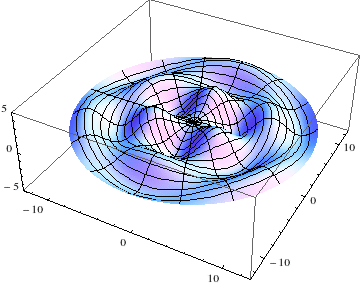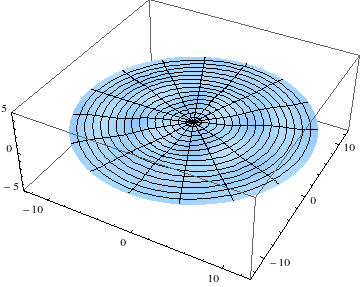
|
Simulation by: Konstantin Makhmutov |
Chladni Figures: Source 1: Sophie Germain (1821). Recherches sur la théorie des surfaces élastiques Source 2: I. Todhunter (2014). Karl Pearson (ed.). A History of the Theory of Elasticity and of the Strength of Materials: Volume 1. Cambridge University Press. p. 153. Source 3: S. P. Timoshenko, (1953). History of Strength of Materials - With a Brief Account of the History of Theory of Elasticity and Theory of Structures Dover Publications, Inc. NY., Chapter V. |
Final remarks
It gets even more interesting when we consider
Partial Differential Equations
Another example: Navier-Stokes equations (imcompressible) \[ \rho \left(\frac{\partial \v}{\partial t} + \v \cdot \nabla \v \right) = -\nabla p + \mu \nabla^2 \v + \F, \quad \nabla \cdot \v = 0. \]
Final remarks
Another example: Navier-Stokes equations (imcompressible) \[ \rho \left(\frac{\partial \v}{\partial t} + \v \cdot \nabla \v \right) = -\nabla p + \mu \nabla^2 \v + \F, \quad \nabla \cdot \v = 0. \]
Fluid simulation by Amanda Ghassaei 🔄 (Reset/Re-start)