Multivariate Calculus
&
Ordinary Differential Equations
Lecture 19
2 Functions of Several Variables
2.2.2 Circles
A circle centered at the origin $(0,0)$ with radius $r$ is given by the equation
$ x^2 + y^2 = r^2.$
2 Functions of Several Variables
2.2.2 Circles
A circle with radius $r$ and center $(h,k)$ corresponds to
$(x-h)^2 + (y-k)^2 = r^2.$
2 Functions of Several Variables
2.2.2 Circles
Example: Sketch the circle $x^2+10x+y^2-4y+20=0.$
Complete the square:
$ \left( \left(x+5\right)^2- 25\right)$ $ + \left( \left(y-2\right)^2-4\right)$ $ +\,20=0$
$\Ra \left(x+5\right)^2+ \left(y-2\right)^2 =9$ $ = 3^2$
Circle of radius 3, centre at $(-5,2)$
Skecht it! 📝

Just touching the heart by Inigo Quilez
2 Functions of Several Variables
2.2.3 Ellipses
In standard form, an ellipse centered at the origin is given by the equation
$\ds \frac{x^2}{a^2} + \frac{y^2}{b^2} =1.$
Let $a\gt b\,$ and define $c\geq 0\, $ by $c^2=a^2-b^2$
$y=0\,$ $\Ra x= a,-a$
$x=0\,$ $\Ra y= \pm b$
2 Functions of Several Variables
An ellipse may also be defined as the set of points in a plane the sum of whose distances from two fixed focal points $F_1$ and $F_2$ is a constant, and you should definitely ask your lecturer to use two pins and a piece of string to demonstrate this.
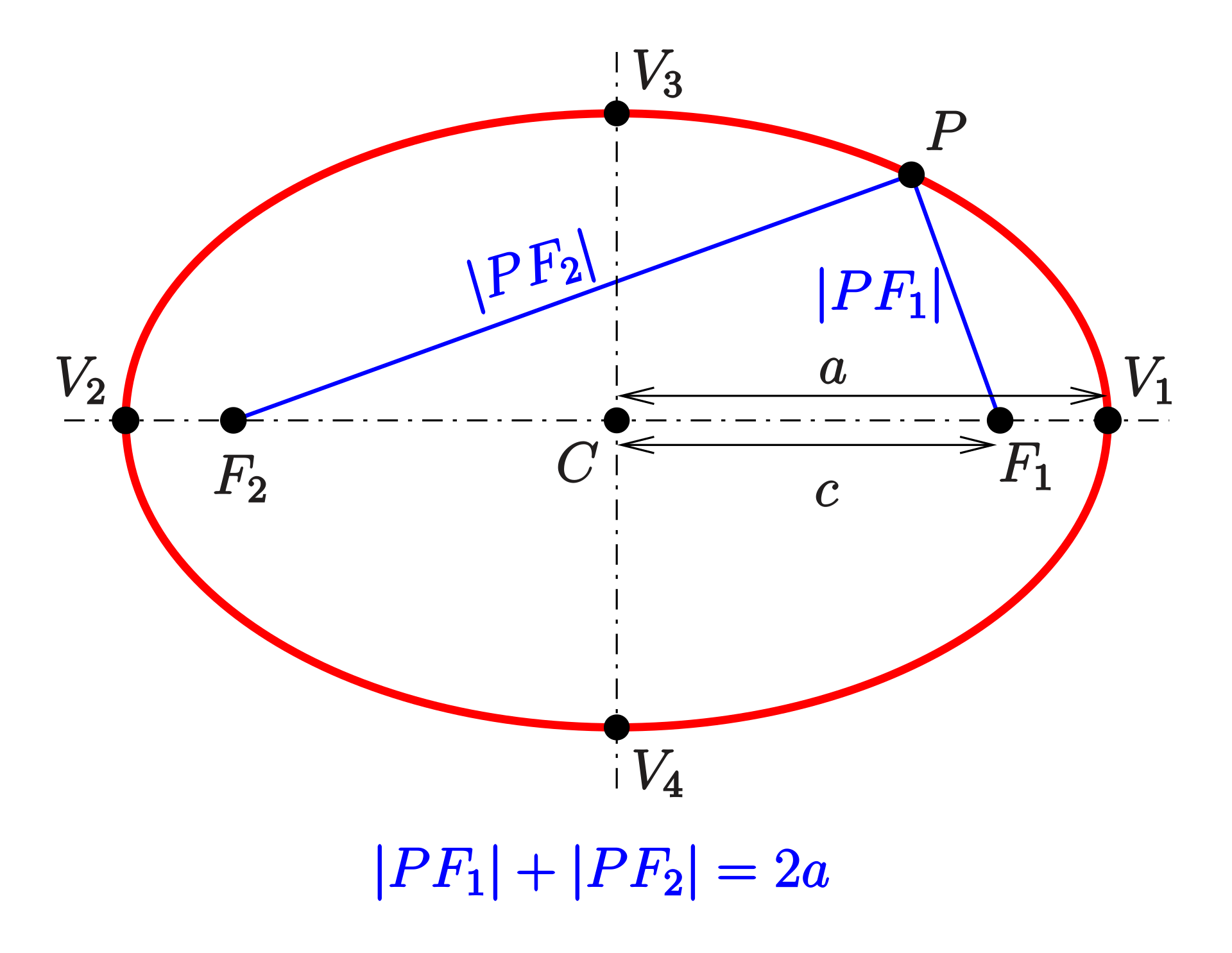
2 Functions of Several Variables
An ellipse may also be defined as the set of points in a plane the sum of whose distances from two fixed focal points $F_1$ and $F_2$ is a constant, and you should definitely ask your lecturer to use two pins and a piece of string to demonstrate this.
2 Functions of Several Variables
An ellipse may also be defined as the set of points in a plane the sum of whose distances from two fixed focal points $F_1$ and $F_2$ is a constant, and you should definitely ask your lecturer to use two pins and a piece of string to demonstrate this.
If $a \geq b,$ then the foci are at $(\pm c,0)$ where $c^2 = a^2 -b^2.$ These lie on the major axis ($x$-axis here). The ellipse intersects the $x$ axis at the vertices $(\pm a,0),$ and the $y$-axis at the vertices $(0,\pm b).$
2 Functions of Several Variables
2.2.3 Ellipses
Question: What is the equation of an ellipse centered at the point $(h,k)$?
$\ds \frac{ \left( x-h\right)^2 }{a^2}+ \frac{ \left( y-k\right)^2 }{b^2}=1$
2 Functions of Several Variables
2.2.3 Ellipses
Example: Sketch the ellipse $x^2-x+9y^2=0$.
Complete the square:
$ \ds \left( \left(x-\frac{1}{2}\right)^2- \frac{1}{4}\right)$ $ +\, 9y^2$ $ =0$
$\Ra \ds \left(x-\frac{1}{2}\right)^2+ 9y^2 =\frac{1}{4}$
$\Ra \ds 4\left(x-\frac{1}{2}\right)^2+ 36y^2 =1$
2 Functions of Several Variables
2.2.3 Ellipses
Example: Sketch the ellipse $x^2-x+9y^2=0$.
$ \ds \left( \left(x-\frac{1}{2}\right)^2- \frac{1}{4}\right)$ $ +\, 9y^2$ $ =0$
$\Ra \ds 4\left(x-\frac{1}{2}\right)^2+ 36y^2 =1$
$\Ra \ds \frac{\left(x-\frac{1}{2}\right)^2}{\left(\frac{1}{2}\right)^2}+ \frac{y^2}{\left(\frac{1}{6}\right)^2} =1$
2 Functions of Several Variables
2.2.3 Ellipses
Example: Sketch the ellipse $x^2-x+9y^2=0$.
$\Ra \ds \frac{\left(x-\frac{1}{2}\right)^2}{\left(\frac{1}{2}\right)^2}+ \frac{y^2}{\left(\frac{1}{6}\right)^2} =1$
If $\, y=0\,$ $\, \ds \Ra x-\frac{1}{2} = \pm \frac{1}{2}\,$ $\, \ds \Ra x = \frac{1}{2}\pm \frac{1}{2}\,$
If $\,\ds x=\frac{1}{2}\,$ $\,\ds \Ra y = \pm \frac{1}{6}$
2 Functions of Several Variables
2.2.3 Ellipses
Example: Sketch the ellipse $x^2-x+9y^2=0$.
$\Ra \ds \frac{\left(x-\frac{1}{2}\right)^2}{\left(\frac{1}{2}\right)^2}+ \frac{y^2}{\left(\frac{1}{6}\right)^2} =1$
If $\, y=0\,$ $\, \ds \Ra x = \frac{1}{2}\pm \frac{1}{2}\,$
If $\,\ds x=\frac{1}{2}\,$ $\,\ds \Ra y = \pm \frac{1}{6}$
2 Functions of Several Variables
2.2.4 Hyperbolas
A hyperbola centered at the origin, with asymptotes $y=\pm b x/a,$ is given by the equation
$\ds \frac{x^2}{a^2} - \frac{y^2}{b^2} =1 \;\;$ or by $\;\;\ds-\frac{x^2}{a^2} + \frac{y^2}{b^2} =1.$
2 Functions of Several Variables
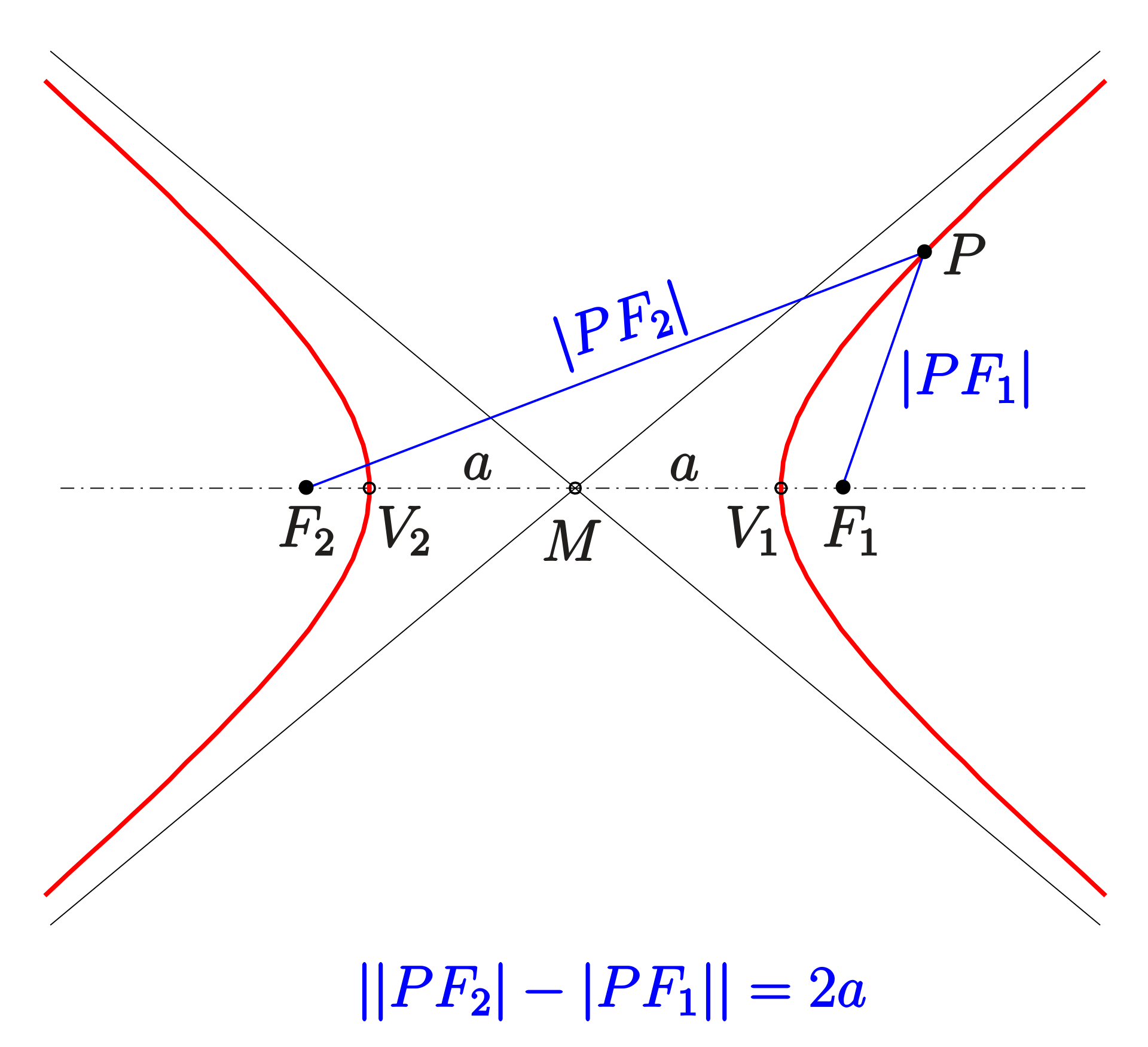
A hyperbola may also be defined as the set of points in a plane, the difference of whose distances from two fixed focal points $F_1$ and $F_2$ is a constant.
2 Functions of Several Variables
A hyperbola may also be defined as the set of points in a plane, the difference of whose distances from two fixed focal points $F_1$ and $F_2$ is a constant.
For such a hyperbola, the foci are at $(\pm c,0)$ and $(0,\pm c)$ respectively, where $c^2 = a^2 + b^2.$
2 Functions of Several Variables
2.2.4 Hyperbolas
Question: What is the equation of a hyperbola centered at the point $(h,k)$?
$\ds \frac{ \left( x-h\right)^2 }{a^2}- \frac{ \left( y-k\right)^2 }{b^2}=\pm1$
2 Functions of Several Variables
2.2.4 Hyperbolas
Example: Sketch the hyperbola $x^2-4y^2=9$.
Standard form:
$ \ds \frac{x^2}{3^2} - \frac{2^2y^2}{3^2}=1$ $\,\Ra \, \ds \frac{x^2}{3^2} - \frac{y^2}{\left(\frac{3}{2}\right)^2}=1$
Centre at $\,(0,0)\,$ and $\,a = 3, b = \dfrac{3}{2}.$
Asymptotes are $\ds y =\pm \frac{\frac{3}{2}}{3}x$ $\ds = \pm \frac{3}{6}x$ $\ds = \pm \frac{1}{2}x$
Skecht it! 📝
Explore the standard form of the hyperbola
2.2.5 Quiz: Can you match each equation with one of the graphs?
| a) $\,x^2-y^2-1=0\quad$ | d) $\,x^2-2x-y+1=0\quad\quad$ |
| b) $\,x+y^2-1=0$ | e) $\,x^2-y^2+4=0$. |
| c) $\,x^2-2x+y^2=0\quad\quad$ | f) $\,4x^2-8x+y^2=0$. |

2 Functions of Several Variables
2.2.6 Main points
-
By completing the square, you should be able to
- sketch any curve of the form $$ax^2 + by^2 + cx + dy + e = 0,$$
- identify this curve as a straight line (or lines), circle, parabola, ellipse or hyperbola, and
- point out its main features such as turning points, asymptotes and intercepts with the $x$- and/or $y$-axes.
- You should also be able to obtain the equation of a curve of the above form from a sketch with features given.
2.3 Contour diagrams
Geographical maps have curves of constant height above sea level, or curves of constant air pressure (isobars), or curves of constant temperature (isothermals). Drawing contours is an effective method of representing a 3-dimensional surface in two dimensions.